How to Use the Different Frequency Dependencies to Manipulate Impedance and Create Various Filter Responses?
To help customers with filter selection, we generally provide a lot of information on what our filters can do. But in this new Filter Basics Series, we are taking a step back to cover some background information on how filters do what they do. Regardless of the technology behind the filter, there are several key concepts that all filters share that we will dive into throughout this series. By providing this detailed fundamental filter information, we hope to help you simplify your future filtering decisions.
In part 2, KNOWLES covered how RF designers can use the different frequency dependencies of capacitors and inductors to manipulate impedance and create various filter responses.
At the most basic level, filters are necessary in RF devices so that unwanted frequencies do not pass through the circuit and cause interreference. While filtering can become quite complex as operating frequencies increase, it can be made much less daunting by having an understanding of how basic filters are built using standard electrical components such as resistors (Rs), capacitors (Cs), and inductors (Ls).
Before we jump into types of filters though, let’s start by looking at how a voltage divider functions. A voltage divider is a passive linear circuit that produces an output voltage (Vo) that is a fraction of the input voltage (Vi). As shown in Figure 1, the voltage divider changes the Vi down to the Vo based on the values of the resistors used, which are R1 and R2 below.
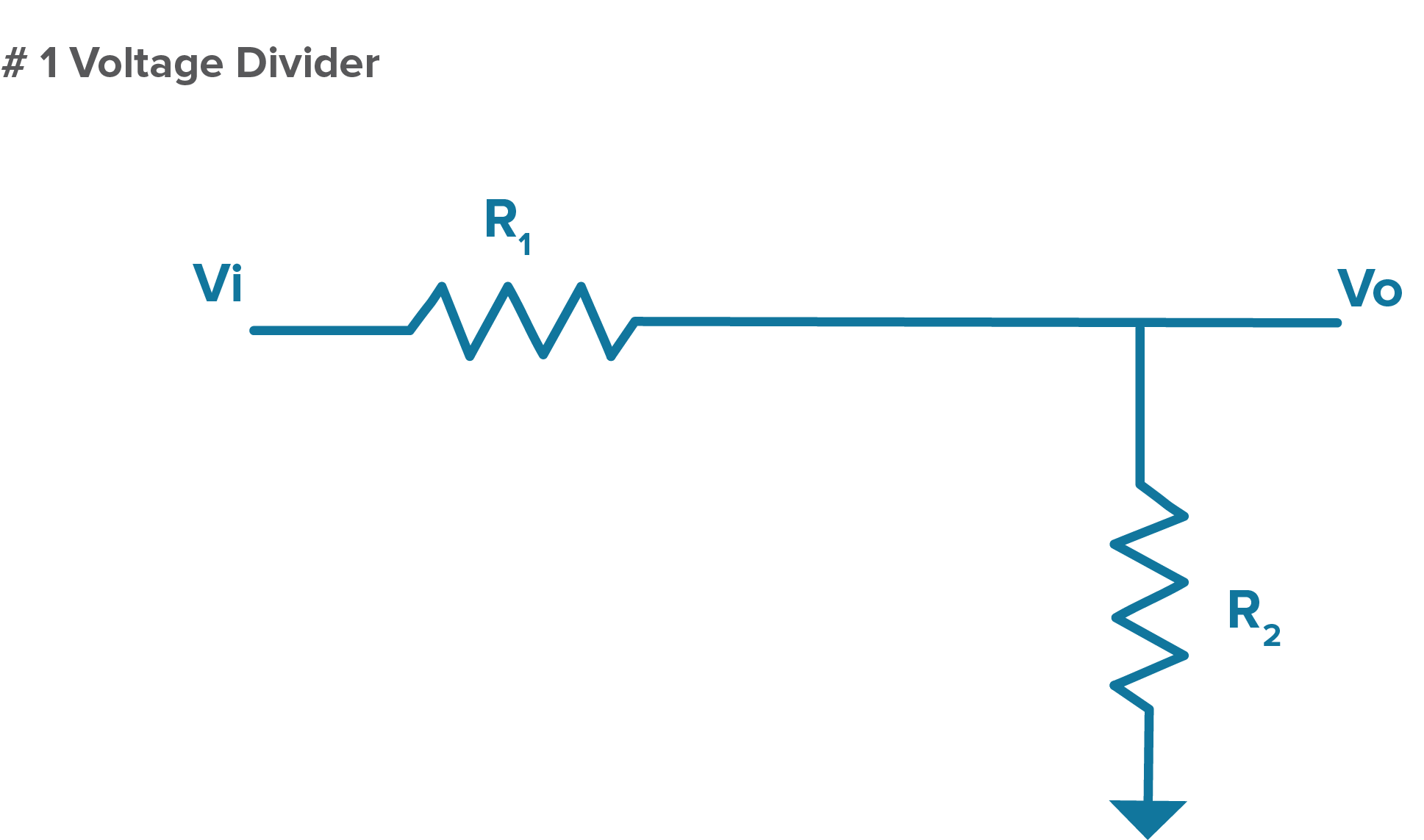
Figure 1. An illustration of the very familiar DC circuit, the voltage divider.
If we start with Ohms Law, which as a reminder, states that electric current is proportional to voltage and inversely proportional to resistance since resistance hinders the flow of current in the circuit, we can derive the following formula for how a voltage divider works:
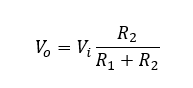
As you can see from the formula above, as R1 grows (or as R2 shrinks) the output voltage will drop.
Swapping Rs and Cs to Turn Our Voltage Divider into a Filter
Now that we know how our simple voltage divider works, let’s look at what happens if we trade out some Rs for Cs. To understand how this works, think back to Part 1 of our series where we covered the fact that inductors and capacitors will act like resistors for AC signals at a certain frequency. Also, in this section we discussed how the impedance of a capacitor will change with frequency and that capacitance can be calculated as follows:
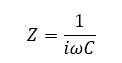
Z = Impedance, Omega = Angular Frequency, i is the imaginary number since we are using complex numbers here, and C = Capacitance.
Thus, for a capacitor, impedance decreases with frequency. So, if we swap R2 for a C as shown in Figure 2, we will have a low-pass RC filter, which is a filter circuit that passes frequency signals below a certain cutoff frequency and blocks frequency signals higher than that point.
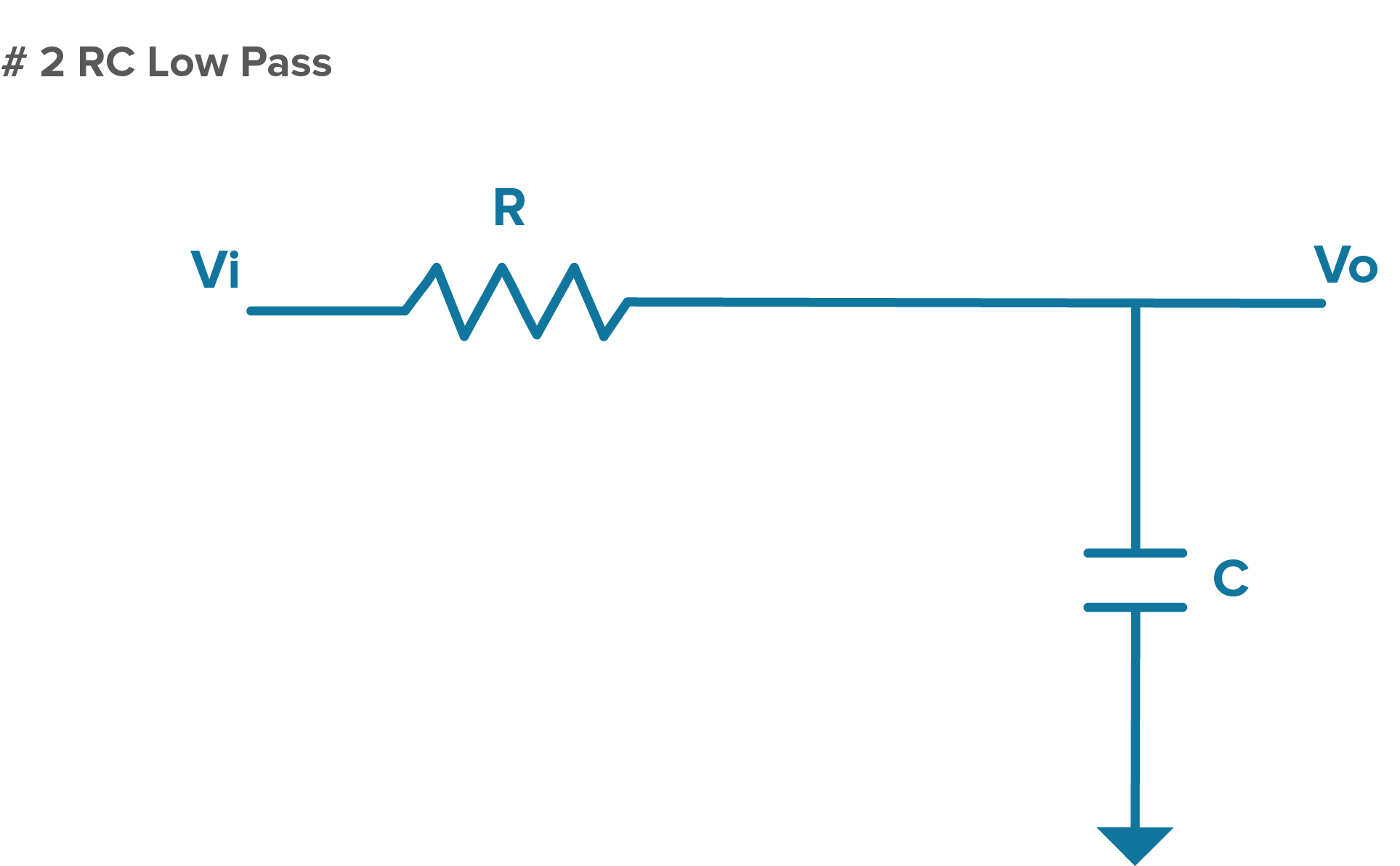
Figure 2. A diagram of an RC low-pass filter.
In the RC low-pass filter, the path to ground goes through a capacitor, which means impedance will decrease with increasing frequency. Therefore, in this circuit, the ratio of the Vi down to the Vo will depend on the values of R and C and the frequency of the signal. With high frequencies, impedance is low and energy is sent to ground as Vi is divided down. Low frequencies see a higher impedance and energy is sent to the output.
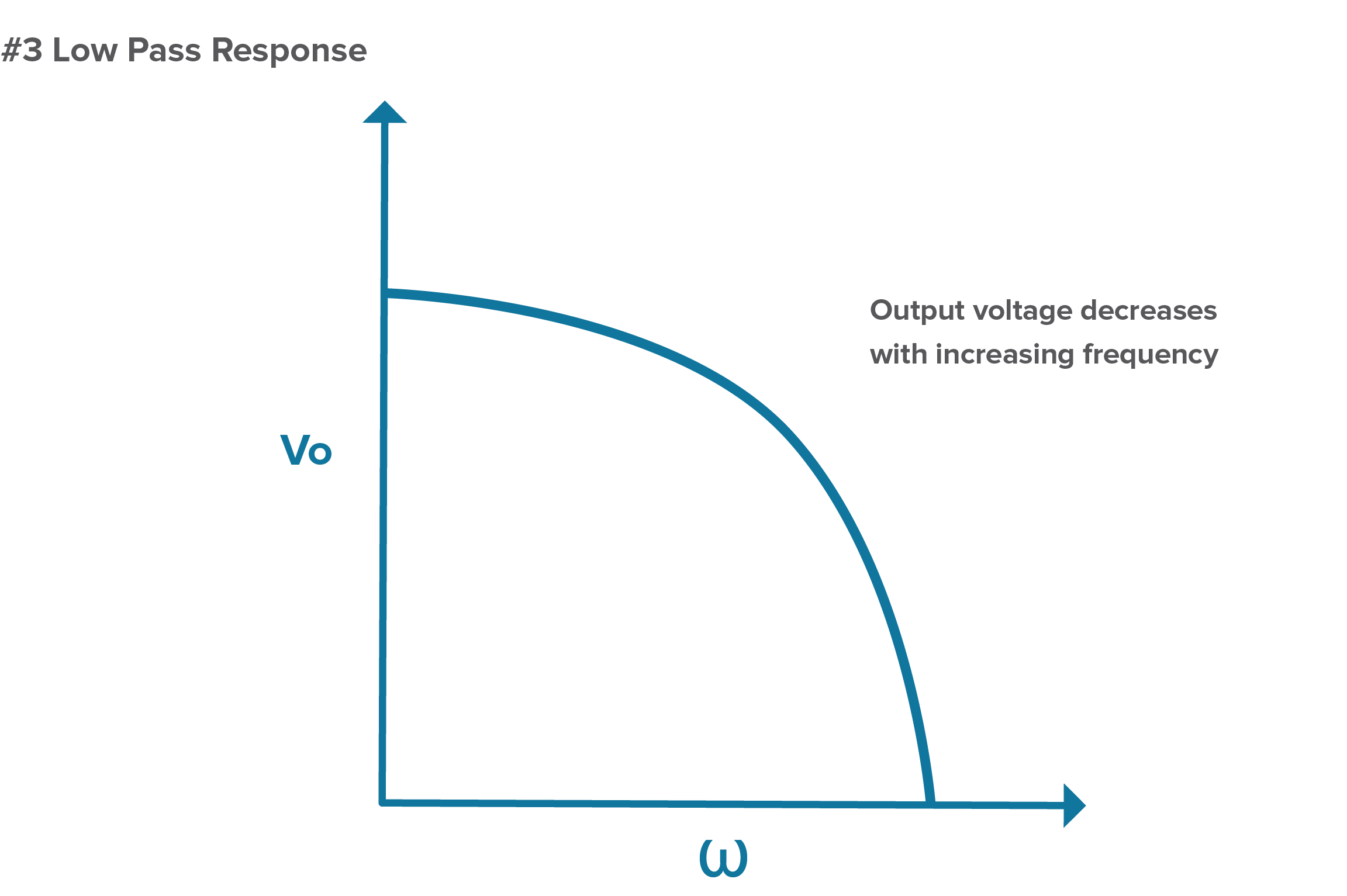
Figure 3. Output voltage decreases with increasing frequency in an RC low-pass filter.
If we do this the other way around and replace R1 with a C, the path to output goes through the capacitor and we get the opposite effect.
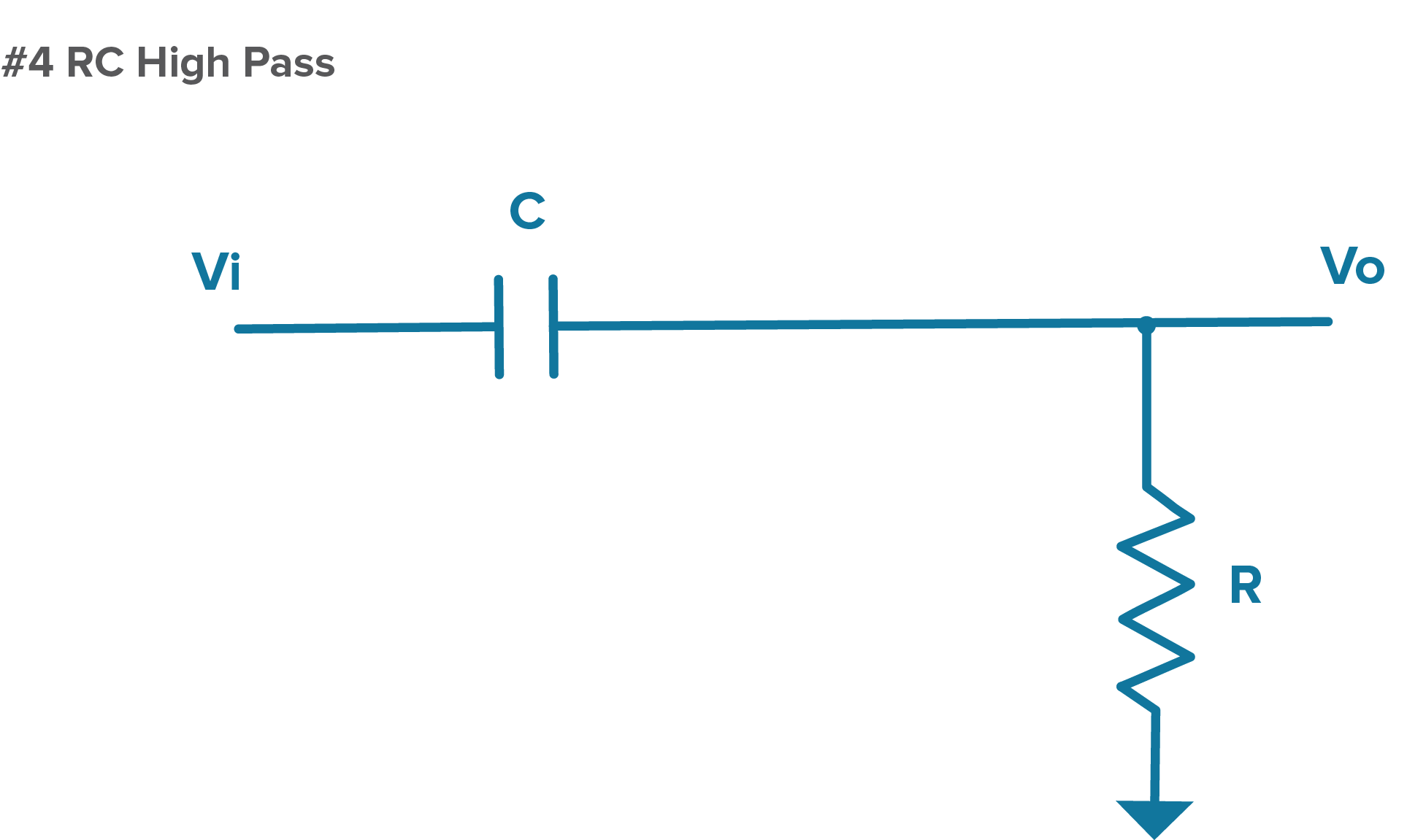
Figure 4. A diagram of an RC high-pass filter.
In this configuration, low frequencies see impedance that is higher than R, so the low-frequency signals go to ground while the high-frequency signals see an impedance lower than R, which means we get a high-frequency output.
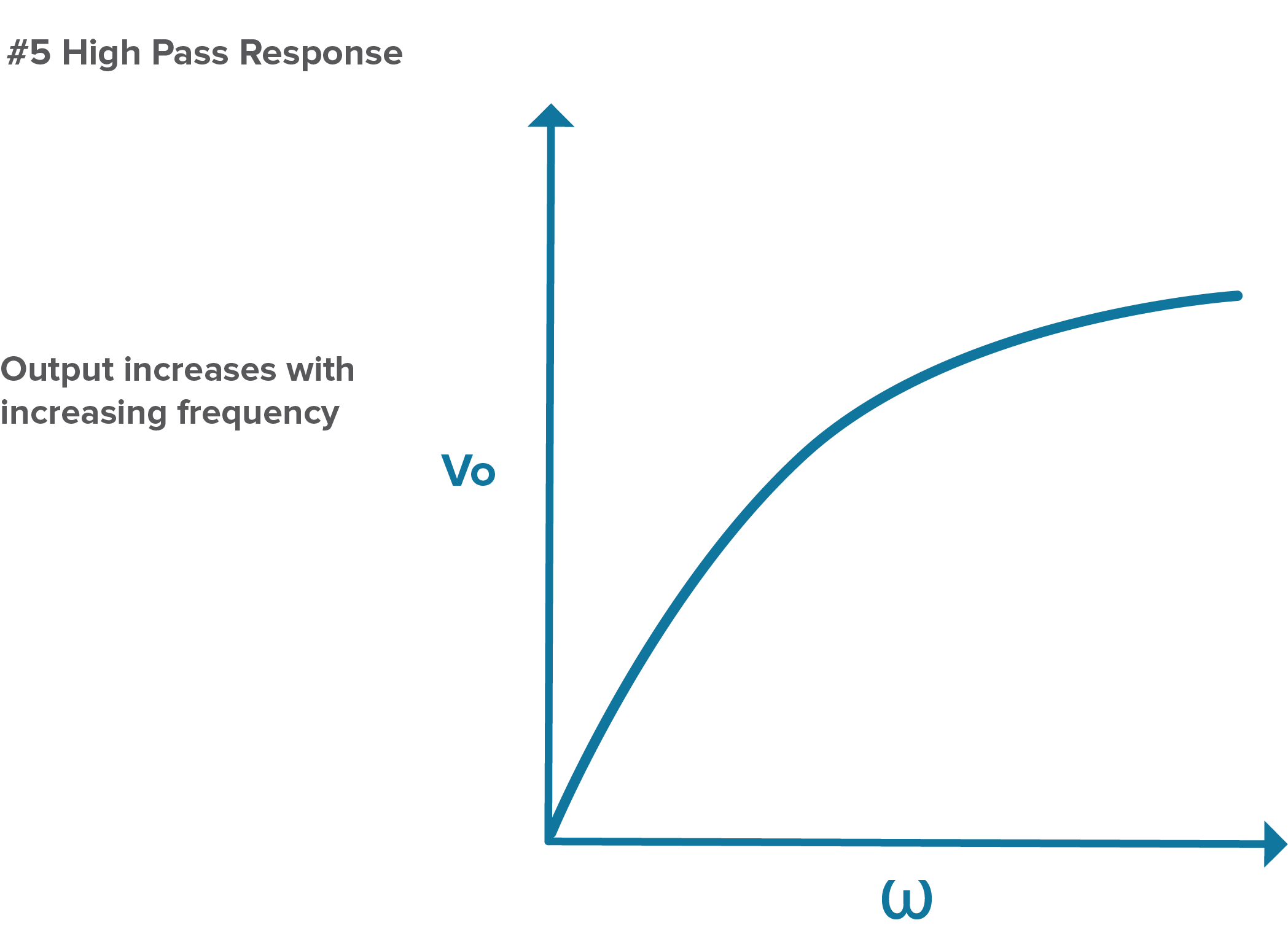
Figure 5. Output voltage increases with increasing frequency when using a high-pass RC filter.
Swapping Cs and Ls to Create Your Desired Filter
Before we jump into talking about how to create different filter configurations by swapping Cs with Ls, let’s recap what we covered in Part 1 on inductors. Inductors have the opposite response to frequency than capacitors. This can be calculated as follows:
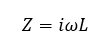
L = Inductance
This means that impedance increases with frequency in an inductor. To create a low-pass filter using an R and L, we can start with an RC high-pass filter as shown in Figure 4 and swap the C for an L. We can also take the same type of approach to design a high-pass filter if we start with a RC low-pass filter as shown in Figure 2 and replace the C with an L. Both examples are illustrated in Figure 6.
Figure 6. In the top diagram, a low-pass filter is converted to a high-pass filter by swapping the C for an L in the path to ground. In the bottom diagram, the high-pass filter is converted to a low-pass filter by swapping the C for an L in the output line.
As it turns out, RC filters don’t provide the best performance in terms of roll off, which is the slope over frequency from passing a signal to blocking it. To improve this, RF designers can combine Cs and Ls, balancing their opposite responses to frequency to build different low-pass, high-pass, and band pass LC filter responses as shown in Figure 7.
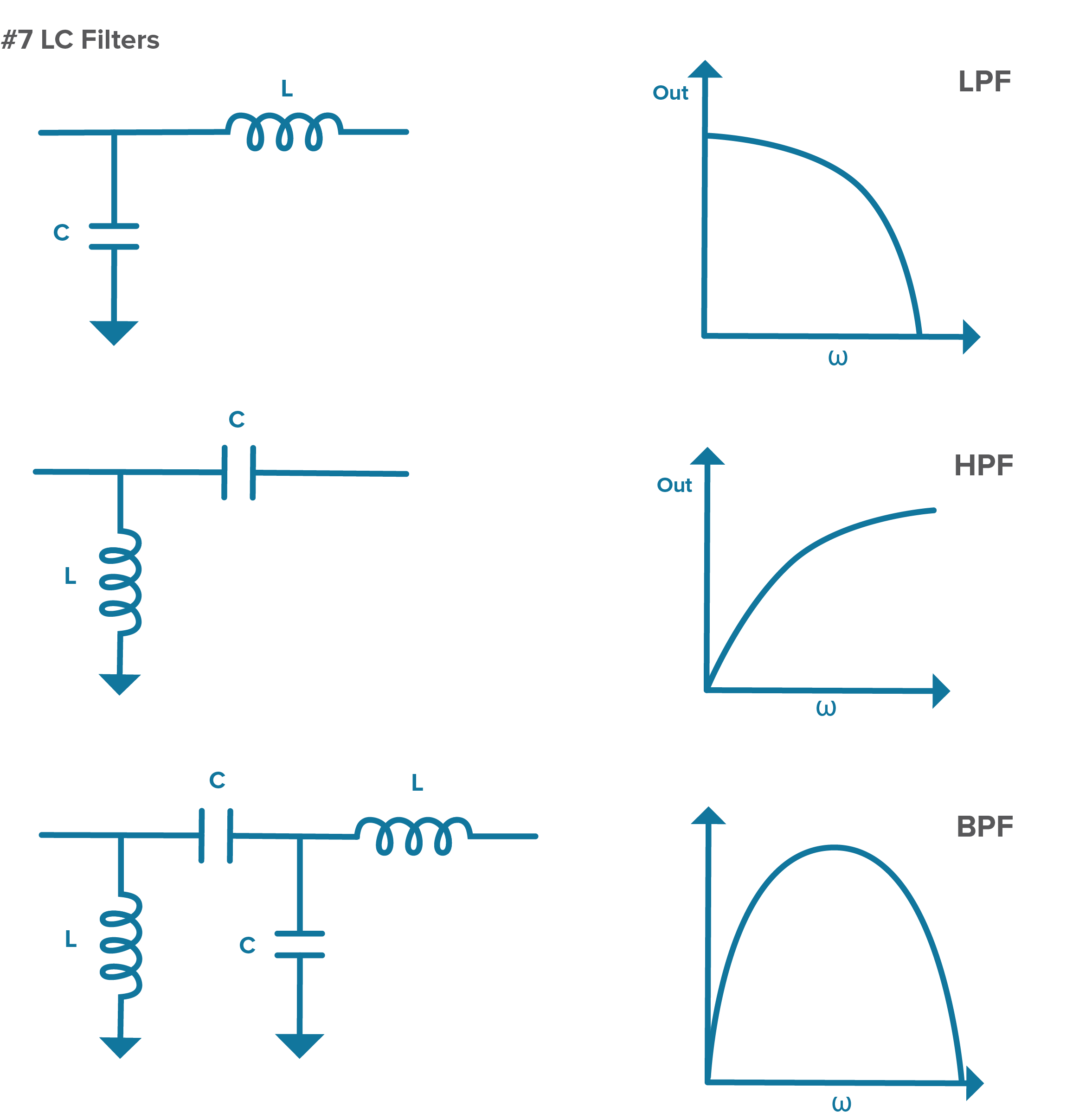
Figure 7. Different types of LC filters and their frequency responses.
Manipulating Impedance to Achieve a Desired Frequency Response in Your Filter
Given that Rs, Cs, and Ls offer different variations on impedance, we can think of designing a filter response as manipulating different impedances to achieve a desired frequency response. Thinking back to the DC voltage divider we started with at the beginning of this post, we can build on this to create a high pass circuit by adding networks of impedance (Zs) using various combinations of RCs and LCs as discussed throughout this post. Figure 8 below shows a high pass circuit where Z1 decreases with frequency and Z2 increases with frequency. In general, by replacing individual Rs, Cs, and Ls with sections of a circuit that have very specific impedance vs frequency behavior, we can create more complex high-performance filters.
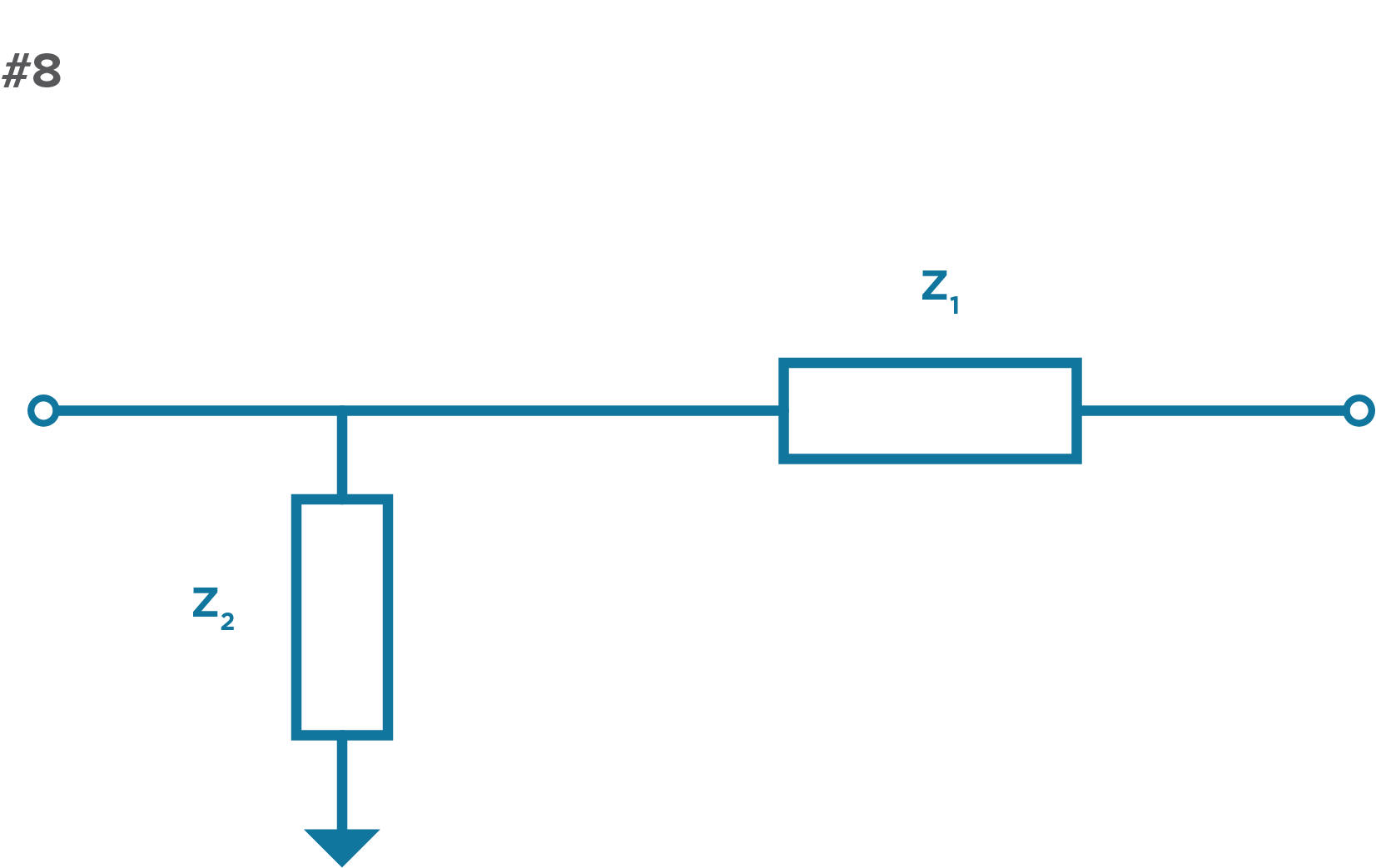
Figure 8. In this example, L and C are replaced with impedances Z1 and Z2.
By breaking down the different ways to use the frequency dependencies of Cs and Ls, you can see how it is possible to get a variety of different filter responses and form simple filters that can serve as the building blocks for more complex filtering needs.
- |
- +1 赞 0
- 收藏
- 评论 0
本文由天星转载自Knowles，原文标题为:Filter Basics Part 2: Designing Basic Filter Circuits，本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。
相关推荐
PCB Design Considerations for High-Performance Filtering in mmWave Applications
RF circuits for applications in the mmWave range (30 to 300 GHz) require high-performance filtering to meet the high-data, high-speed functionality that operating at these higher frequencies promises. However, filters for devices operating in the mmWave range will not function optimally if your printed circuit board (PCB) is not configured appropriately. To address these complex issues, when starting a new circuit design for a mmWave application, Knowles recommends carefully evaluating the following design factors for your PCB assembly
设计经验 发布时间 : 2022-04-25
Switch Filter Banks for Agile RF Receiver Design in Radar
This is the third installment in our RF Components for Radar series. In the first installment, we provided an overview of the key functional units in radar, including duplexing, filtering, power amplification, waveform generation, low-noise amplification (LNA), receiving and analog-to-digital conversion (ADC). Here, we’ll focus on a particular form of filtering technology: switch filter banks.
设计经验 发布时间 : 2024-06-14
Knowles（楼氏电子）射频滤波器（定制产品）选型指南
目录- Company Profile Technology Capabilities Ceramic Technology Package Option Ceramic Resonators Cavity Filters Lumped Element Filters Bandpass Filters Bandreject Filters Lowpass and Highpass Dual Bands / Multi-Bands & Diplexers Multiplexers Specialty Filters Space Heritage
型号- 942274,943440,943441,943442,943443,918565,936908,940694,943480,932199,938738,936754,930257,941699,938533,935061,938576,938571,935265,934450,935264,935384,935263,942225,931406,940121,933827,936669,932342,936741,935535,935579,943503,943504,941008,942658,943627,936740,938044,942330,942331,942651,943501,943502,935838,938949,939606,936735,940989,932413,937501,938556,DR03F36Q1550AYB,933984,938635,908704,937144,936333,923787,943452,942320,942080,930615,931396,940417,937017,938663,931190,938660
Knowles（楼氏电子）微波产品选型指南
目录- Microwave Products Microstrip Filter Overview Filter Catalog Part Number Structure Bandpass Filter Lowpass Filter Highpass Filter Cavity Filters Resonators Notch Filters Custom and Build-to-Print Integrated R-C Networks Couplers Gain Equalizers mmWave Filters Speciality Kits SatCom Offerings User Guidelines:Chip and Wire or Hybrid Assembly User Guidelines:Surface Mount Recommend Reflow for Surface Mount
型号- FPC06302,H100XHXS,PDW08607,PDW08605,PDW08606,AEQ2234,B076MB6S,L288XC3S,PDW07630,AEQ03042,PDW08604,B148LA2S,B280LB0S,B280MD1S,L220XH5S,FPC07643,B056MB5S,B028LB7S,B099NC4S,B191KA1S,B080MB5S,B061MB6S,B033ND5S,PDW07069,B168MB1S,DEB-B274MB1S,DEB-B385MDOS,B083LB6S,L204XF4S,PDR05848,B119LB1S,B065NC5S,B210LA0S,AEQ03055,J30BLBA032LX1,B20BLSBN01,N016MD9S,FHC10290,FHC10291,FHC10292,FHC10293,B012MD5S,FHC10288,FHC10289,J30BJBA002LX3,AEQ05470,AEQ02199,AEQ05471,AEQ05472,B052NC5S,C079KB1S,AEQ05467,AEQ05468,AEQ05469,PDR06120,L157XG3S,B148QF0S,H140XHXS,B350NB2S,B105MB5S,PDW06984,PDR06390,B056RC4S,C142KB0S,PDW09692,B047MC5S,B094LA2S,FPC06630,B032ND5S,B102MC1S,FPC06078,B285LB2S,FPC06077,FPC06076,PDW07948,B115NB4S,B119MB1S,B111NC4S,B230LA0S,AEQ05246,L254XF3S,PDR06380,FPC06075,FPC06074,B042OD4S,FPC06073,B060NC5S,B142LA2S,B145LB1S,B380KA1S,B274MB1S,FPC06882,FPC06881,J30BJBA032LX1,B180MA1S,PDW06407,PDW06089,PDW06400,B192NB2S,PDW06401,H120XHXS,B220LA0S,B280LA0S,B280MC1S,N012ME9S,B118LB4S,B291MB0S,B070MB6S,FHC09097,B121MB4S,FHC09096,B040RG9S,B070NC5S,B393KD0S,J30BLBA002LX3,B095MB1S,B057MC5S,B20BHSBN01,FPC07183,FPC07182,B120MB1S,FPC07181,FPC07180,FPC06149,L128XH4S,FPC07234,AEQ3042,B024RF2S,B100MC5S,AEQ2199,FPC06701,FPC06700,DEB-B259MC1S,PDW08324,PDW08323,B031ND5S,B207LA0S,H080XHXS,B116NC5S,H168XHXS,FPC06154,FPC06153,PDW06933,AEQ3055,FPC07803,FPC07802,L065XG9W,L065XG9S,B138LA2S,B138MB1S,B190MB1S,FPC06152,B055NC5S,FPC06151,FPC06150,B200LA0S,PDW06011,J30BJBA022LX2,B058MD7S,AEQ2050,FPC06164,B28BJBFN01,PDW05758,B089NC4S,FHC09101,B028RF2S,FHC09102,AEQ05510,B260MB2S,FPC06719,B150OG0S,PDW06041,B385MD0S,B062MC55,L050XF9S,AEQ02234,AEQ06042,B149MC1S,B289KA0S,PDW06398,PDW06399,PDW06038,B381KD0S,J30BLBA012LX4,B040MB5S,B112MB1S,B240LA0S,FPC09291,B259MC1S,H160XHXS,B161LA0S,B081RC0S,B250LA0S,B280MF1S,L185XF4S,B096QC2S,FPC06913,B305LA0S,L157XF3W,L060XD9S,L095XG9S,B479KB0S,L185XF4W,B120RF0S,B039NC5S,FPC07337,B160KA1S,B279KB1S,J30BLBA022LX2,H182XHXS,B144MB1S,PDW07691,B038NC4S,B424MEZS,L117XH4S,B097MB0S,L117XH4W,B050ND4S,B016MD6S,B28BHBFN01,B28BTBFN01,B127MB2S,B165LA1S,J30BJBA012LX4,H060XHXS
Knowles Precision Devices Introduces the SFSW Series of Hermetic, Panel-Mount EMI Filters
Knowles Precision Devices has expanded EMI filter offerings to include hermetically sealed EMI filters that attenuate unwanted EMI signals while allowing desired signals to pass. SFSW series filters were designed to preserve signal integrity and ensure reliable operation in high-reliability applications with strict electromagnetic compatibility standards.
产品 发布时间 : 2024-11-02
Knowles（楼氏电子）EMI滤波器选型指南
目录- General and Technical Introduction SM EMI Filters Panel Mount EMI Filters Discoidals, Planar Arrays and Special Filters
型号- SFAJL5000471MX,SFBDC5000220ZC,SFSUC5000150ZC0,SFBDT5000102MX,SFCMC5000333MX,SFBCC5000102MX,SFJGL5000224MX,SBSGC5000102MX,SFCDC5000681MX,SFBLL5000333MX,SFABL5000102MX,SFKKC5000330ZC,SFBML5000100ZC,SFAKT1000104MX,SFBML5000151MC,SFJNL2K00331MC,SFBCL5000681MX,SFCML5000221MC,SFJGL2K00471MC,SFKKT5000103MX,SFJNL2K00682MX,SFJGL1K00223MX,SFSUC5000680MC0,SFABC2000683MX,SFJGL1K00683MX,SFAKT5000681MX,SFBMC5000102MX0,SFABC5000103MX,SFBCL1000104MX,SFLMC1000104MX,SFBCP5000442ZX,SFBDT5000333MX,SFJNL2K00222MX,SFJGC2000105MX,SFJGP5000944MX,SFAJC5000472MX,SFBCP5000200ZC,SFAAC,SFCMC5000104MX,SFSUC5000683MX0,SFBDL5000470ZC,SFBCC5000333MX,SFKKC5000152MX,SFKKT5000101MC,SFCML5000683MX,SBSGC5000333MX,SFBDP5001N36MX,SFBDP5000443MX,SFBDC5000100ZC,SFBMP5000302MX,SFBDT5000331MC,SFTMC5000470ZC,SFABL5000333MX,SFBDT5000222MX,SFCDL5000471MX,SFBDC5000151MC,SFBDP5000201MC,SBSGC5000222MX,SBSMP5000152MX,SFAJC5000221MC,SFJNL2K00102MC,SFKKT5000332MX,SFKBL5000470ZC,SFKKL5000220ZC,SFLMP0500304MX0,SFAJC1000104MX,SFBCL5000101MC,SFBLL5000331MC,SFJGC5000334MX,SFCDL,SFCDC5000101MC,SFABL5000682MX,SFAJL5000153MX,SFBDP5000663MX,SFJGC3K00151MC,SFCDP,SFCMC5000222MX,SFJGC2K00472MX,SFKKT5000223MX,SFBML5000153MX,SFBCC5000150ZC,SFJNC2K00103MX,SFBCC5000682MX,SFBLL5000222MX,SFCDC,SBSMC5000472MX,SFABL5000150ZC,SFBDT2000473MX,SFBMT2000683MX,SFBMC5000472MX,SFCDC5000332MX,SFLMT5000100ZC,SFBCL5000332MX,SFLMC5000101MC,SFCDL1000474MX,SFJNL1000155MX,SFTMC5000333MX,SFLML5000680MC,SFAAC5000100ZC,SFCDC5000683MX,SFBCC2000473MX,SFKKL5000100ZC,SFABL5000680MC,SFLML5000153MX,SFKKT5000681MX,SFKKL5000151MC,SFABC5000101MC,SFAAC5000151MC,SFKKT5000221MC,SFBCC5000680MC,SFABL2000473MX,SFJNC0500335MX,SFTMC5000150ZC,SFSUC5000223MX0,SFCDP5000942MX,SFAKL2000683MX,SFCDL5000153MX,SFUMC5000220ZC,SFABC5000332MX,SFAKL5000332MX,1206Y1000103MXTE07,SFLML2000473MX,SFLMT5000151MC,SFLMC5000221MC,SFBLC5000332MX,SFBLC2000683MX,SFDPP0500944MX0,SFSRC5000220ZC0,SFAAC5000471MX,SFCMC5000102MX,SFLMP5000942MX,SFBDP5000301MC,SFCMC2000224MX,SFBCL2000683MX,SFCML5000681MX,SFAJC5000681MX,SFAJL5000100ZC,SFBLL5000102MX,SFCML5000472MX,SFKKT1000104MX,SBSPP1000682MX,SFBCL5000221MC,SFBDT5000150ZC,SBSGC5000682MX,SFAJL5000151MC,SFCDC5000221MC,SFBCP5000202ZX,SFLMC5000223MX,SFBML5000220ZC,SFABC5000223MX,SFJGP1K0136NMX,SFBDP5000203MX,SFKKT2000683MX,SFAKC5000470ZC,SFLMC5000332MX,SFCMC5000150ZC,SFKBL5000682MX,SFAAC5000153MX,SBSMC1000224MX,SFBDC5000153MX,SFJNC2K00332MX,SFLMT5000220ZC,SFAKT5000472MX,SFBLL5000150ZC,SFJGL5000104MX,SFLML5000471MX,SFSTC5000101MC0,SFJGC2K00103MX,SFAJL5000331MC,SFTMC,E01,SFBCP1000443ZX,E03,SFAKC5000152MX,SFAAC2000473MX,SFCDL5000102MX,E07,SBSGP5000222MX,SFBMC5000681MX,SFBMT5000220ZC,SFUMC0500154MX,SFJGL2K00331MC,SFUMC5000680MC,SFAJL5000682MX,SFKBL5000222MX,SBSGP0500224MXB,SFAJL5000222MX,SFBMP2000943MX0,SFKBC5000103MX,SFAJC2000683MX,SFJGP2K00302MX,SFKBL5000331MC,SFCDC5000154MX,SFKKC5000470ZC,SFBCC5000471MX,SBSMP5000472MX,SFJGL2K00682MX,SFBLC5000220ZC,SFABL5000471MX,SFKBC5000223MX,SFCMC5000473MX,SBSMC5000683MX,SBSMC5000223MX,SFJNC2000105MX,SFLML5000220ZC,SFJGL2K00222MX,SFAKL5000220ZC,SFTMC5000330ZC,SFBMP5000442MX,SFCML0500684MX,SFLMT2000683MX,SFBLC5000151MC,SFKBL5000102MX,SBSPP1000222MX,SFSUC1000334MX0,SFTMC2000473MX,SFCMC,SFAKT5000152MX,SFBML0500154MX,SBSGC5000473MX,SFCDL5000222MX,SFCML,SFBML5000471MX,SFAAC5000220ZC,SFAJC5000330ZC,SBSGP5000102MX,SFBLL5000680MC,SFJNL5000154MX,SBSMC5000332MX,SFUMC5000101MC0,SFLML5000151MC,SFCMC5000680MC,SFBMC1000104MX,SFJGL0500335MX1,SFBLC5000681MX,SFAKT2000683MX,SFLMC5000103MX,SFKBL2000473MX,SFBMT1000104MX,SFCDL5000331MC,SFBCC5000102MX0,SFBDT5000470ZC,SFAKL5000100ZC,SFJGP2K00942MX,SFLMC2000683MX,SFLML5000100ZC,SFLMT5000103MX,SFBLP0500943ZX,SFJGC2K00332MX,SFAKL5000151MC,SFAKL5000681MX,SFBLC5000100ZC,SFBMP5000662MX,SFCML5000103MX,SFKBL5000333MX,SFBMP5000940ZC,SFUMC5000151MC,SBSGC5000153MX,SFSTC5000472MX0,SFBMC5000330ZC,SFSTC5000102MX0,SFAJL0500154MX,SFKBL5000150ZC,SFKBC5000221MC,SBSPP1000102MX,SFBCL5000472MX,SFCMC5000331MC,SFBDT5000102MX0,SFUMC5000100ZC,SFCDL5000680MC,SFJGC0500335MX,SFAKL5000472MX,SFKBC5000101MC,SFBMT5000153MX,SFSUC5000332MX0,SFABL,SFBLC5000472MX,SFCDC5000472MX,SFBCP5000941ZX,SFBDL5000330ZC,SFBCL5000152MX,SFCDC5000152MX,SFABC,SFCDP5000302MX,SFAKL1000104MX1,SFJGC2K00681MC,SFBMT5000100ZC,SBSMC2000154MX,SBSMP2000104MX,SBSGP0500224MX,SFJNL1K00153MX,SFSRC0500473ZX0,SFAJL2000683MX1,SFBLC5000153MX,SFJGP2000205MX,SFBDP5000661MC,SFAKL5000153MX,SFJGL2K00102MC,SFKKL2000683MX,SFCDL5000682MX,SFBMP50013N6MX,SFBMT5000151MC,SFCML5000332MX,SFCDL5000473MX,SFKBC5000332MX,SFBDL5000152MX,SFBLP2000203ZX,SBSMC5000103MX,SFBMP5000202MX,SFAKT5000330ZC,SFBLL0500154MX,SFJNC3000684MX,SFJGL1000225MX,SFBDC2000683MX,SFUMC5000471MX,SFCML5000101MC,SFSUC5000220ZC0,SFBML5000680MC,SFAJL5000680MC,SFBLL5000682MX,SFBMC5000152MX,SFAKC5000330ZC,SFCML5000223MX,SFSTC2000473MX0,SFBDP5000441MC,SFJGC1K00333MX,SFAJC5000152MX,SFUMC5000153MX,SFCMC5000682MX,SFJGP1K00943MX,SFBDC5000331MC,SFBDT5000330ZC,SFLMT2000473MX,SFBDC5000222MX,SFBDP5000941MX,SFCDP5000661MC,SFBCC5000151MC,SFCDP5000201MC,SFBCC5000100ZC,S
Knowles（楼氏电子）符合AEC-Q200标准的汽车级电容器选型指南
目录- AUTOMOTIVE GRADE CAPACITORS INTRODUCTION GENERAL AND TECHNICAL INTRODUCTION MLC CAPACITORS SM EMI FILTERS
型号- 1808JA250102JCTSP,1808JA250102JXTPY2,1808JA250102GJTSYS,2220YA300563KSTS3X,085J2500101JHT,1812Y1000334MXTE03,1812Y5000474KJTWS2,1206Y1000473KNT,1206Y0500224KXT---,2220JA250102JXTB16,1206Y1000103MXTE07,1808JA250102KJTSYX,0805Y1000103KST---,1210Y2000103KCT---,1808JA250102GJTS2X
Filter Basics about Different Approaches to Q Factor
In part 7 of this series, Knowles performs a deep dive on the different ways you can think about the Q factor for the components going into your filter or your filter as a whole.
应用方案 发布时间 : 2022-07-31
Knowles‘ Microstrip Filters Offer a High Repeatability and Temperature Stability from -55℃ to 125℃
Since Knowles acquired Integrated Microwave Corporation (IMC) in 2020, Knowles has an extended its range of RF and microwave filtering solutions to include a wide variety of ceramic coaxial resonators, lumped element filters, and cavity filters from the VHF to the Ka-band.
原厂动态 发布时间 : 2023-04-04
电子商城
现货市场
授权代理品牌：集成电路
授权代理品牌：分立元件
授权代理品牌：接插件及结构件
授权代理品牌：部件、组件及配件
授权代理品牌：电源及模块
授权代理品牌：电子材料
授权代理品牌：仪器仪表及测试配组件
授权代理品牌：电工工具及材料
授权代理品牌：机械电子元件
授权代理品牌：加工与定制
我要提问
登录 | 立即注册
提交评论