了解ADC的幅度量化误差

时间： 2024-01-31 来源：TOPPOWER官网

代理服务

技术支持

采购服务

ADC将输入值转换为一组离散级别中的一个值，并输出数字代码以指定量化级别。量化过程会给系统带来一些误差。

本文将通过将斜坡输入应用于量化器来研究量化误差。然后，我们将看一个示例，其中量化误差类似于噪声源。此外，我们将讨论使用噪声源对量化误差进行建模的优点。我们将在本文的下一部分继续讨论。在那里，我们将研究允许我们使用噪声模型的假设，并且我们将使用获得的模型来表征量化误差的影响。

理想的ADC

理想的单极三位ADC的传递函数如图1所示。

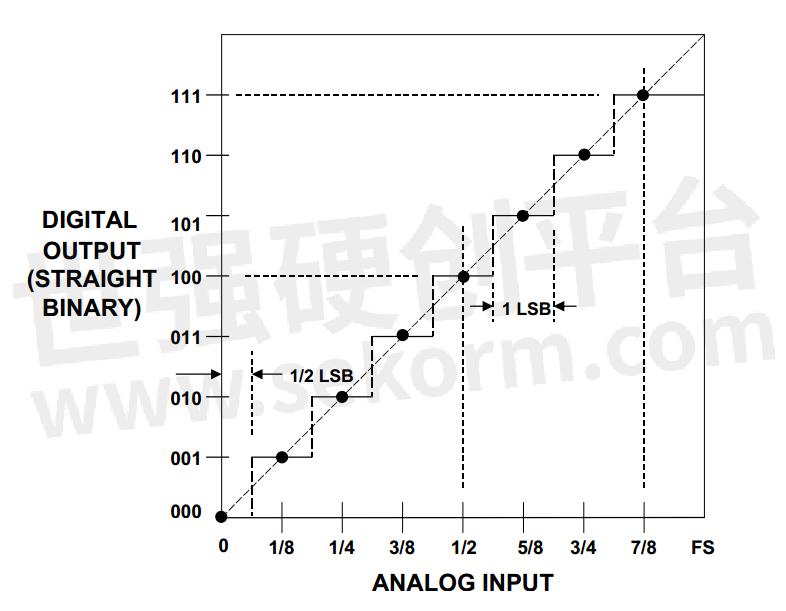
图 1

模拟输入的满量程(FS)值被分为八个相等的间隔（用?、1/4、...表示）。在这些间隔的中点，存在从一个数字输出值到下一个数字输出值的转变。除个和一个台阶外，其他台阶的宽度都等于FS/8。步长(FS/8)还指定输出数字代码的有效位(LSB)的模拟值。因此，如果我们将上述ADC的输出应用于理想的数模转换器（图 2），代码001将产生模拟值FS/8，代码010将产生FS/4，依此类推。

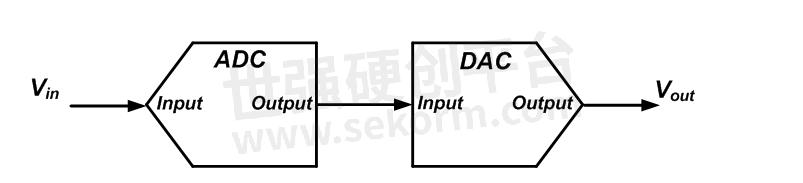
图2

幅度量化误差

这里重要的一点是，给定的数字代码代表一系列模拟输入值；输入的幅度被量化。例如，从FS/16到3*FS/16的所有输入值都由一个输出代码（代码001）表示。如果我们将 ADC 的输出连接到理想的三位 DAC（图 2），代码 001 将产生模拟值 FS/8。因此，从 FS/16 到 3*FS/16 的模拟值由单个模拟值 FS/8 表示。因此，即使是理想的幅度量化也会引入一些误差。该误差称为量化误差 (V q )，可以通过从 DAC 输出 (V out ) 中减去 ADC 输入 (V in ) 来计算，如下图 3 所示。

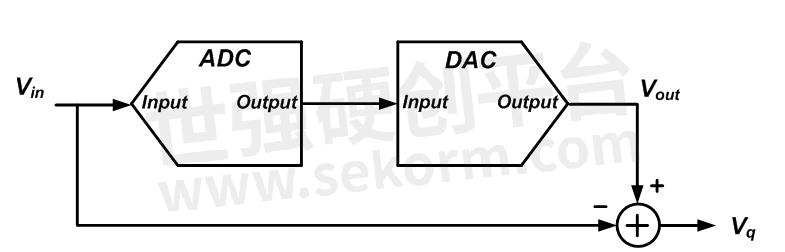
图3

斜坡输入的量化误差

让我们将斜坡信号应用于上述设置的输入，并更仔细地检查量化误差。图 4 中的蓝线显示了应用于输入的斜坡。此外，该图以红色显示了我们在 DAC 输出中获得的量化电平。

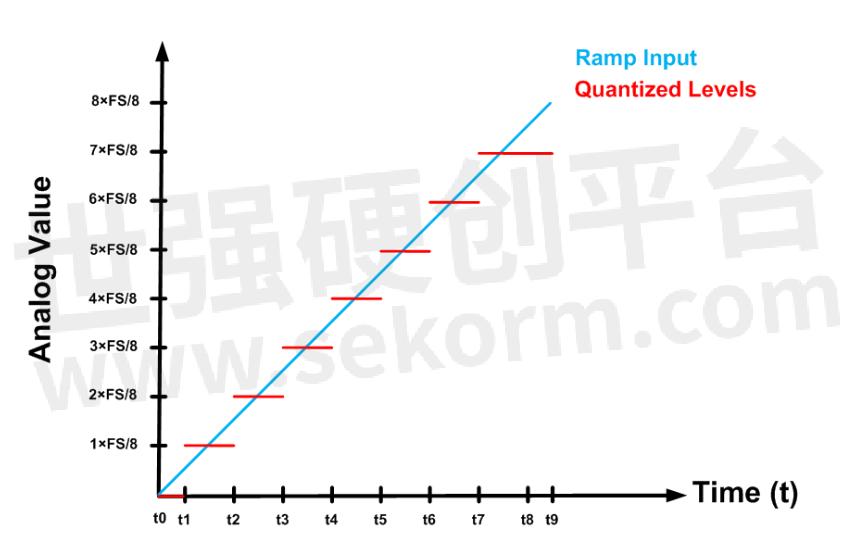
图4

在t 0和t 1之间，输入小于FS/16。考虑到图 1 的输入输出特性，ADC 输出为 000，这给出了量化模拟值 V out = 0。如图 5 所示，此间隔的量化误差从 0 到 - ? ? FS/8（负半个 LSB）。

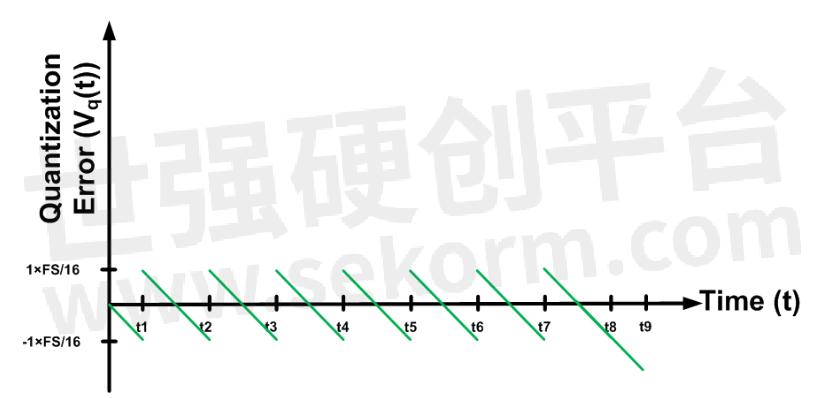
图5

在t 1和t 2之间，输入大于FS/16且小于3FS/16。ADC 输出为 001，给出量化模拟值 V out = FS/8（见图 1 和 4）。对于此间隔，量化误差范围为 + ? ? FS/8 到 - ? ? FS/8（参见图 5）。同样，我们可以找到其他量化级别的误差值，如图 5 所示。请注意，除了一个级别之外，量化误差始终在 ± FS/16（半个 LSB）之间。

现在我们可以使用图 5 来计算斜坡输入的量化误差的均方根 (RMS) 值。在区间 T 1 < t < T 2内定义的函数 f(t) 的 RMS可通过以下等式获得：

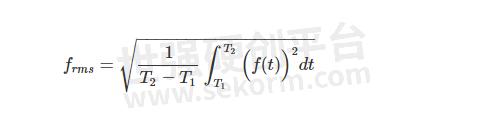
对于图 5 的误差波形，我们有：

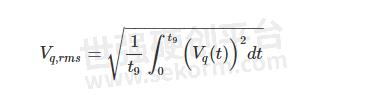
为了简单起见，我们忽略波形的部分 (0 < t < t 1 ) 和部分 (t 8 < t < t 9 )。随着量化器分辨率的提高，忽略这两部分而引入的误差会减小。我们获得：

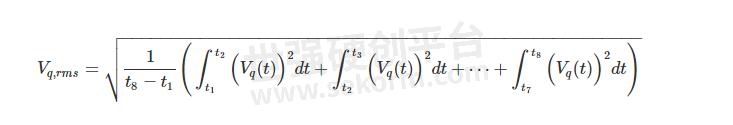
上式中的积分对应于同一信号的时移版本。时间平移不会改变曲线下的面积（或等效地，其积分）。因此，这些积分项是相等的。由于 t 2 -t 1 = t 3 -t 2 = …= t 8 -t 7，我们可以将上式简化为：

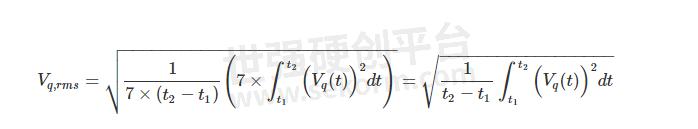
公式1

我们可以直接计算上面的积分。然而，为了使计算更简单，我们假设t 2 -t 1 = T并对波形应用-T/2的时移。因此，我们可以简单地计算 V q ,new (t)的 RMS，如下图 6 所示。

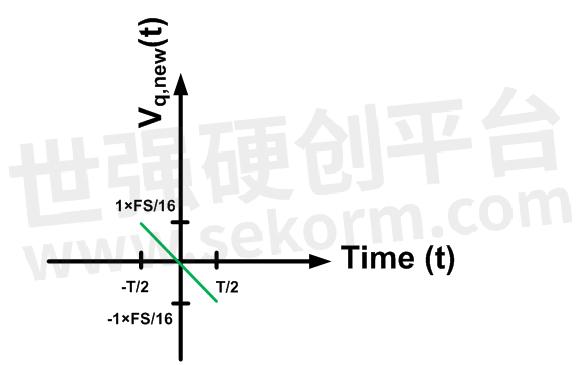
图6

因此，方程 1 可以重写为

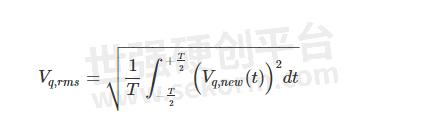
公式2

其中 V q ,new (t) 由以下等式给出：

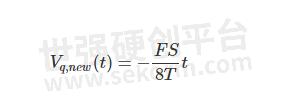
将此方程代入方程 2 并计算得出

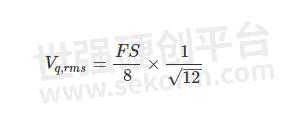
我们知道FS/8是LSB的模拟值。因此，RMS 误差由以下等式给出：

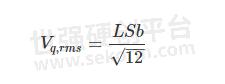
这是一个重要的结果，我们稍后将再次推导它（在本文的第二部分），从不同的角度看待问题。

让我们总结一下迄今为止的发现：我们发现，即使是理想的幅度量化也会在系统中引入一些误差，称为量化误差。为了研究该误差的一些特性，我们应用了斜坡输入并观察到误差的 RMS 与 LSB 值成正比。此外，如图 5 示例所示，量化误差始终在 ±LSB/2 之间。提高量化器的分辨率将减少 LSB 和误差项。此外，忽略图 5 中波形的部分 (0 < t < t 1 ) 和部分 (t 8 < t < t 9 )，我们观察到误差的平均值为零。另请注意，对于给定的输入值，我们可以计算出误差的准确值。

更复杂输入的量化误差

尽管上述讨论使我们能够深入了解量化误差的某些属性，但它基于一个不切实际的假设，即输入是斜坡。让我们看另一个例子。这次我们对离散余弦信号 x[n]=0.99cos(n/10) 进行量化，如图 7 所示。

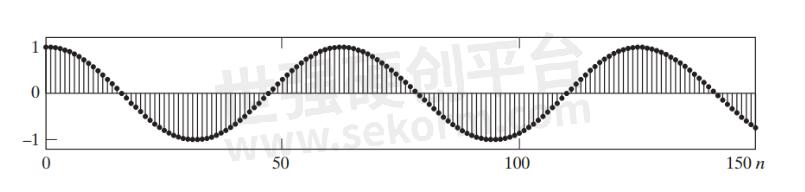
图 7图片由离散时间信号处理提供。

如果我们对该信号应用 8 位量化器，量化误差序列将如图 8 所示。

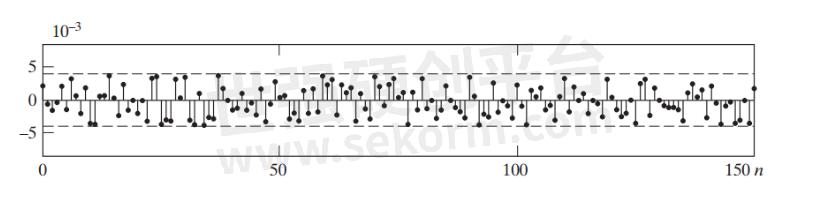
图 8图片由离散时间信号处理提供。

与斜坡输入的情况不同，此示例的误差似乎不遵循某种模式，并且计算 RMS 误差并不容易。将此示例的输入余弦与错误序列进行比较，我们观察到以下内容：

输入是单频信号，但误差信号的频率内容似乎有很大不同。它的变化很快，因此我们期望它具有高频成分。

我们无法通过目视检查识别输入余弦和错误序列之间的联系。错误序列似乎与输入不相关，并且从一个样本到下一个样本随机变化。

正如我们在斜坡输入示例中观察到的那样，我们知道量化误差信号并不是真正随机的，实际上可以针对给定的输入值进行计算。但是，如果我们可以在某些假设下将量化误差建模为随机信号呢？量化误差的幅度在 ±LSB/2 之间，这可能是一个很小的值，特别是当我们处理高分辨率量化器时。现在，如果这个低幅度信号以不可预测的方式变化，人们可能会得出结论，它类似于我们通常在不同电路和系统中遇到的噪声源。

将量化误差建模为噪声源的优点

将量化误差视为噪声源可以使问题简化很多。我们知道如何分析特定类型的噪声源对线性时不变 (LTI) 系统的影响。噪声源的瞬时值通常是不可预测的，因此时域分析是不可能的。然而，我们可以长时间观察噪声，并利用测量结果找到噪声的统计模型。例如，噪声源的一个有用特征是其“功率谱密度”（PSD），它使我们能够深入了解不同频带中噪声的平均功率。具有噪声信号的PSD，因此，假设可以通过噪声源对量化过程进行建模，我们只需要找到噪声模型的功率谱密度，并用它来表征误差对系统性能的影响。在这种情况下，我们可以使用图 3 的模型来描述具有加性噪声源的量化过程，如图 9 所示。如您所见，量化值 (V out ) 等于输入( V in )加上模拟量化误差 (V q )的噪声信号。

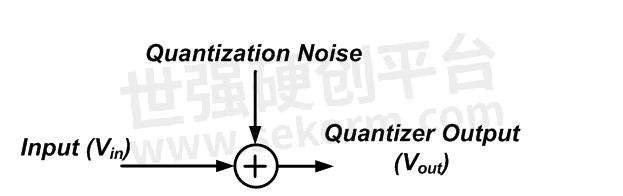
图9

在本文的下一部分中，我们将研究将量化误差建模为噪声源的条件。然后，我们将深入研究所获得模型的一些重要特征，并使用它们来分析量化误差对系统性能的影响。

结论

即使是理想的幅度量化也会在系统中引入一些误差，称为量化误差。该误差的 RMS 与 LSB 值成正比。看来，我们可以在某些假设下将量化误差建模为噪声信号。如果可能的话，这可以显着简化分析量化误差对系统性能的影响。

发送到邮箱 |
+1 赞 0
收藏
评论 0
| 转发至：

本文由咪猫转载自TOPPOWER官网，原文标题为:了解 ADC 的幅度量化误差，本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。

平台合作

提交评论

全部评论（0）

暂无评论

ADC偏移误差和ADC增益误差实例应用

了解ADC的偏移和增益误差规范，例如ADC传输函数，并通过ADC偏移误差和ADC增益误差示例进行操作。

2023-12-15 - 设计经验代理服务技术支持采购服务

如何理解和优化模数转换过程中的量化误差？

在本系列文章中，我们深入探讨了模数转换（ADC）和数模转换（DAC）的关键性能标准，重点分析了量化误差的成因、影响以及如何通过提高分辨率和采用适当的滤波器来优化转换质量，确保数字信号能准确反映模拟世界的现象。

2024-05-23 - 设计经验代理服务技术支持采购服务

ADC与DAC测试，验证静态和动态特性的方法与分析

本文介绍了如何通过输入输出测试来验证模数转换器（ADC）和数模转换器（DAC）的静态和动态特性，包括失调误差、增益误差、积分非线性（INL）和微分非线性（DNL）的测量，以及使用频率分析来确定ADC的动态范围。

2024-05-19 - 设计经验代理服务技术支持采购服务

解析ADC模数转换器中积分非线性（INL）的调整误差、和相对精度

本文中，TOPPOWER介绍了另一种定义INL误差的方法，即拟合线方法。在这种情况下，使用穿过所有代码的直线作为参考线。

2024-03-21 - 技术探讨代理服务技术支持采购服务

一文解析ADC总谐波失真

本文TOPPOWER来为大家介绍ADC总谐波失真，希望对各位工程师朋友有所帮助。ADC中的缺失代码如何导致ADC输出失真。这种失真将导致输入信号的谐波出现在ADC的输出中。虽然具有缺失代码的ADC确实会产生大量谐波失真，但缺失代码并不是谐波失真的来源。ADC输出中的谐波失真是由ADC特性中存在的任何非线性引起的。

2024-12-22 - 技术探讨代理服务技术支持采购服务

如何模拟ADC的前端？

对于SAR-ADC来说，模拟是一件棘手的事情。目前还没有完整的转换器模型可以准确地模拟整个设备。您拥有的资源是一个模拟SPICE文件，它可以模拟模拟输入引脚的稳定性。拥有此工具的幸运在于，您拥有一个强大的工具来解决关键、困难的转换器问题之一。

2024-07-10 - 技术探讨代理服务技术支持采购服务

解析ADC工作原理和分类

ADC是模数转换器（Analog-to-Digital Converter）的缩写，它是一种电子设备，用于将模拟信号转换为数字信号。模拟信号是连续变化的信号，而数字信号是离散的信号，由一系列离散数值组成。ADC广泛应用于各种领域，如通信、控制系统、传感器技术和音频处理等。在许多现代电子设备中，ADC都扮演着非常重要的角色，因为它可以帮助设备处理和分析来自外部世界的模拟信号。

2024-02-28 - 技术探讨代理服务技术支持采购服务

如实显示嵌入式微控制器的自动代码生成？

本文介绍了电气工程师在嵌入式控制系统开发中面临的挑战，并提出了通过控制建模和自动代码生成来提高开发效率和质量的方法，同时强调了PLECS工具在简化微控制器编程和I/O外设配置中的作用。

2024-05-05 - 设计经验代理服务技术支持采购服务

如何分析模数转换器在实际应用中的误差？

在设计测量系统时，我们需要充分了解不同的误差源以及它们对整体精度的影响。误差分析使我们能够自信地选择组件并确保系统满足精度要求。本文TOPPOWER通过不同的例子深入讨论ADC系统误差分析。

2023-12-28 - 设计经验代理服务技术支持采购服务

如何使用带有嵌入式ADC的CDBCAPTURE系统？

CDBCAPTURE系统可用于从嵌入式模数转换器 (ADC) 收集数据。因此，可以测量、分析和量化模拟前端的系统性能。通过分析测量的性能，可以识别、隔离噪声源并采取纠正措施。这里使用CDBCAPTURE作为工程工具，减少系统测试和集成期间的开发时间。另一个应用程序可以在生产中使用CDBCAPTURE来测试成品并验证系统性能。

2023-11-01 - 设计经验代理服务技术支持采购服务

TOPPOWER（顶源科技）电源模块/开关电源选型指南

公司介绍 DC-DC 隔离定电压输入电源 DC-DC 隔离宽电压输入电源 DC-DC 非隔离电源 AC-DC 板载电源 AC-DC 机壳基板型开关电源 AC-DC 导轨式型开关电源

TOPPOWER - AC‐DC ENCLOSED&OPEN FRAME TYPE SWITCHING POWER SUPPLY,DC-DC CONVERTERS,AC-DC封闭式和开放式框架式开关电源,开关电源,NON-ISOLATED DC-DC POWER CONVERTERS,模块电源,DC‐DC ISOLATED CONSTANT INPUT POWER CONVERTERS,DC-DC 隔离定电压输入电源,ISOLATED WIDE INPURT POWER CONVERTERS,DC-DC隔离式宽输入电源转换器,POWER CONVERTER,交直流DIN导轨式开关电源,DC-DC转换器,ISOLATED WIDE INPUT POWER CONVERTERS,交直流变换器,导轨电源,AC-DC DIN RAIL TYPE SWITCHING POWER SUPPLY,电源模块,DC-DC隔离式恒定输入功率转换器,DC-DC 隔离宽电压输入电源,DC-DC非隔离宽输入电源转换器,AC-DC 机壳基板型开关电源,DC-DC ISOLATED CONSTANT INPUT POWER CONVERTERS,PCB MOUNTABLE POWER CONVERTERS,SWITCHING POWER SUPPLY,隔离式宽输入电源转换器,AC-DC 导轨式型开关电源,AC-DC ON-BOARD REGULATED POWER CONVERTERS,DC-DC 非隔离电源,AC-DC车载稳压电源转换器,开关电源供电,非隔离式DC-DC电源转换器,AC-DC ON-BOARD REGULATED POWER CONVERTERS,DC-DC NON-ISOLATED WIDE INPUT POWER CONVERTERS,AC-DC ENCLOSED & OPEN FRAME TYPE SWITCHING POWER SUPPLY,AC-DC 板载电源,AC-DC CONVERTERS,AC‐DC DIN RAIL TYPE SWITCHING POWER SUPPLY,DC-DC ISOLATED WIDE INPUT POWER CONVERTERS,TP50DC,TPK-SAR,TPC/PWF-150-XS,TPI-2W,TP15AT,TKA-W25,TPV-W25,TP15AS,TPR/DG-30-XS,TPR/SDR-240-XS,TP03AA,TP35DC,TP15ACS,TPC/PS-60-XS,TPR/DG-15-XS,TPET,TP30ACS,TP50DG,TPR/NDR-U75-XS,TP78XX-0.5,TP15AC,TP30AT,TP30AU,TPVT,TP15AL,TPK-3W,TP03AR,TP10AC,TP2L-3W,TPVT-2W,TP03AZ,TPC/GKF-320-XS,TPE2,TP10ACS,TPE1,TPV1,TPV-SAR,TP03AC,TPD-W25,TP03AD,TPC/PDF-1200-XS,TPR/NDR-U120-XS,TPV2,TP03AL,TPET-2W,TPC/PWF-100-XS,TPB,TPC/LPD-100-XS,TPD,TPG,TPF,TPR-W25,TPI,TPH,TP2L-2W,TPK,TPJ,TPAT-W2,TPL,TKE-W25,TPAT-W5,TP06DB,TP06DE,TPS,TP25DG,TPT,TPC/LR-150-XS,TP50AU,TPR/SDR-360-XS,TP05DB,TP05DA,TP20DC,TP78XX-2,TP20DB,TP2L-1W,TP20DD,TP78XX-1,TPR-W5,TPV2-W5,TPR/SDR-120-XS,TPH-3W,TPC/PDF-800-XS,TP78LXX-1,TPAT,TP20AC,TPAT-2W,TP10DB,TP10DA,TP10DC,TP20ACS,TP20ACL,TPG-3W,TPC/LR-200-XS,TP05ACS,TPET-W2,TP40DC,TPET-W5,TP01AZ,TPJ-2W,TKE-W5,TP05AS,TP05AR,TPA2,TP06DA,TP12AC,TPC/PDF-600-XS,TKA,TPA1,TP50AE,TP40DG,TPR/NDR-U240-XS,TKE,TP05AZ,TP05AD,TP05AF,TPC/LR-350-XS,TP05AC,TP20AT,TP05AL,TP20AU,TPD-W5,TPC/GKF-200-XS,TPL-3W,TPVT-W5,TPC/LR-50-XS,TPC/PD-25-XS,TP30DB,TPR/SDR-75-XS,TPLE-W5,TP2L-6W,TP15DC,TP30DG,TP15DB,TPLE-W1,TPC/NE-350-XS,TP30DC,TP50DH-300DH,TPLE,TPC/LR-35-XS,TPD-2W,TP08DA,TP10AG,TP10AF,TPV1-W5,TP10AS,TPR/SDR-480-XS,TP50DH-300,TP10AT,TP78LXX-1.5,TPVT-W2,TP02AZ,TP25AU,TP03DB,TP03DA,TPA-W25,TPV-W1,TPB-1W,TP06AC,TP15DD,TPD-3W,TPR-1W,TP30-60AH,TP40AU,TPC/PS-35-XS,安防,INDUSTRIAL CONTROL,汽车,NEW ENERGY,电力,INSTRUMENTATION,医学电子学,仪器仪表,MEDICAL ELECTRONICS,铁路运输,TECHNOLOGY,通信,电动汽车,军事系统,物联网,医疗器械,SECURITY INDUSTRY,军工,MILITARY SYSTEMS,能源,技术,充电桩,ELECTRIC VEHICLES,COMMUNICATIONS,工控,新能源,IOT,CHARGING PILES,ELECTRIC POWER,仪表,电子,证券业,医疗,仪器,轨道交通,电动车辆,RAIL TRANSPORTATION

2023/8/4 - 选型指南代理服务技术支持采购服务