流量传感器（2-1）超声流量传感器-信号采样率的影响及相关处理插值模拟部分的代码更新

时间： 2024-06-18 来源：AMPHENOL SENSORS（安费诺传感器学堂公众号）

技术问答

选型帮助

研发客服

商务客服

我们之前在《流量传感器(2)—超声流量传感器，相位差和相关性原理》中曾留了一个问题：如果采样频率不一样，模拟的结果会怎么样？不知道大家有没有时间去运行测试一下，反正小编尝试了。测试的结果（但不是最终结论，请根据实际应用进行调整）下文会提到。

在小编上次关于超声流量的相关信号处理的模拟中，用到了插值的方式，不过由于没有经过太多的测试，在后续测试过程中，发现当声速为4500m/s的模拟流体的流速不超过15m/s时，都没有什么问题；但是当模拟的流速超过15m/s之后，两组模拟信号的相位差超过了180°时，获取相关性序列中对应的时间值时，发现取值结果为负数。

相位差180°，这本身没有问题，但是由于数据的相关性处理函数是个偶函数，对称于中点，所以在数据相关性处理中，当两路信号的相位差超过180°前后时，因为两路测试信号是正余弦形式，相当于其中一路信号序列在相对于另外一路信号序列移动的时候，在某个相对处的相关计算结果，可以找到另外一个错位的对方有相同的相关处理结果，然而在查找标识相位偏差所对应的最大值时间序列值时，测试代码优先输出了最左侧编号是负数的相位序列，实际应该输出相关性序列中点右侧的最大值所对应的时间序列值。结果可想而知，计算的流速变成了负数。修改后的代码中，计算流速时，使用的相关性序列是整个相关结果序列的右边部分，就解决了输出流速突然变成负数的问题。

另外，实际的超声波接收信号并不会是从头至尾都是理想的正余弦，因此，我们看到的模拟信号似乎也是太过于理想。这里我们稍微加了点料，让稳定的信号后面加上了快速衰减。在进行模拟信号相关性处理的时候，之前我们使用的是直接死磕方式的计算，这里调整为快速傅里叶计算（FFT）。所以，这里我们将模拟代码作了以下调整，顺便作了在不同采样频率下的模拟测量值比较：

在原来的模拟超声波接收信号的生成数据中，加入最后衰减的部分；
在生成的相关性序列中，只取中间点右侧的一半作为分析处理部分；
图像输出时，仍然输出全部的相关性序列；
在生成相关性序列时，需用了FFT的模式（原先的选用的直算的方式）；
降低“采样频率”到5MHz，然后采样插值的方式进行相关性处理。

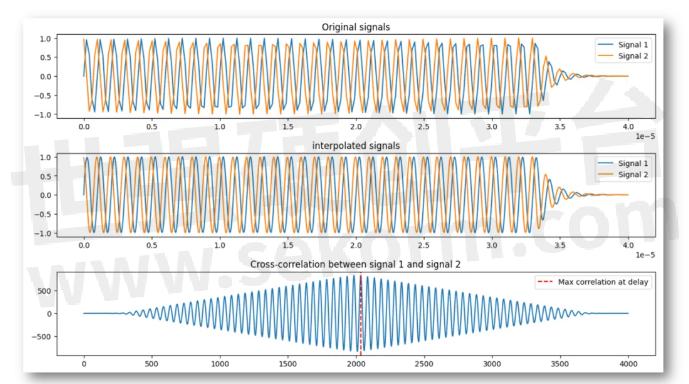
上图模拟的是16m/s下，5MHz采样率，得到的输出值：

T1_0: 4.5617943222309144e-07

Length of t lags: 2000Ts Delayed cycles: 23 ,

Delayed time: 4.6e-07degree(相位差，角度): 165.6

Sample time interval(采样间隔时间): 2.0e-08

Estimated velocity: 16.134001(m/s)

不同采样率，不同模拟流速下的模拟输出比较（都有插值）

从模拟结果来看，较高的采样率确实可以获得较高的测量精度，而低的采样率，虽然适用了插值提高了测量精度，但是插值运算毕竟是基于我们设定了波形的形态进行的。实际应用，还是要根据实际需求和情况配置相关的软硬件功能。

另外需要说明的是，在整个信号相关性处理的模拟过程中，这里并没有将相关性结果序列归一化后输出，而是使用直接结果的方式。

小编还要留一个问题：如果插值处理中标识插值点数的参数有变化的时候，模拟结果会出现什么变化？欢迎大家测试并留个回复。

修改之后的模拟代码其中：模拟代码中的噪声部分是被注释掉的：

import numpy as np

import matplotlib.pyplot as plt

from scipy.signal import correlate

import math

from scipy.interpolate import interp1d

def cor_demo():

try:

# Parameters

c = 4500 # Sound speed in the fluid in m/s

d = 0.5 # Pipe diameter in meters

theta = math.pi / 6 # Angle of the emitted ultrasound wave, in radians. 30 degrees here.

L = d / math.cos(theta) # The sound path length in meters parallel to the flow direction

v = 16 # Fluid velocity in m/s

f = 1e6 # Frequency of the signal in 1MHz

T = 1 / f # Period of the signal in s

Fs = 5e6 # 采样频率为5MHz

Ts = 1/Fs # 采样间隔

# Calculate time delay caused by flow velocity

time_up = L / (c - v * math.sin(theta)) # Time of flight upstream

time_down = L / (c + v * math.sin(theta)) # Time of flight downstream

print("T1_0:",time_up-time_down)

t_delay = 2 * L * v * np.sin(theta) / (c**2 - v**2 * np.sin(theta)**2)

# Time array

# 返回一个从0到period*T范围内的有num_samples个元素的一维数组，数组中的数值是等间距分布的

period = 40

num_samples = period*T/Ts

t = np.linspace(0, period*T, int(num_samples))

t_max = t.max()

t_start_decay = t_max * 5/6

# 定义信号衰减准则 - 衰减系数一般由物质的特性决定

attenuation_coefficient = 10e5

# Signals

stationary_s0 = np.sin(2 * np.pi * f * t[t<t_start_decay])

stationary_s1 = np.sin(2 * np.pi * f * (t[t<t_start_decay] - t_delay))

decay_so = np.sin(2 * np.pi * f * t[t>=t_start_decay])* np.exp(-attenuation_coefficient * (t[t >= t_start_decay] - t_start_decay))

decay_s1 = np.sin(2 * np.pi * f * (t[t>=t_start_decay]-t_delay))* np.exp(-attenuation_coefficient * (t[t >= t_start_decay] - t_start_decay))

#s0 = np.sin(2 * np.pi * f * t)* np.exp(-attenuation_coefficient * t)

#s1 = np.sin(2 * np.pi * f * (t - t_delay))* np.exp(-attenuation_coefficient * t) #*2.0 # Signal 1

s0 = np.concatenate([stationary_s0, decay_so])

s1 = np.concatenate([stationary_s1, decay_s1])

"""

noise0 = np.random.normal(0, 0.5, s0.shape)

noise1 = np.random.normal(0, 0.5, s1.shape)

s0 = s0 + noise0

s1 = s1 + noise1

"""

# Define interpolation factor

interp_factor = 10

# New time vector after interpolation

t_new = np.linspace(t.min(), t.max(), t.size * interp_factor)

# Create a function based on the original signals, which can be used to generate the interpolated signals

interp_func_s0 = interp1d(t, s0, kind='cubic')

interp_func_s1 = interp1d(t, s1, kind='cubic')

# Generate the interpolated signals

s0_new = interp_func_s0(t_new)

s1_new = interp_func_s1(t_new)

# 计算Cross-correlation，并找到最大值对应的位置

#correlation = correlate(s1, s0, method='direct', mode='full') # old

correlation = correlate(s1_new, s0_new, method='fft', mode='full')

# 找出该序列的长度 len_corr 和其中间点 mid_index

len_corr = len(correlation)

mid_index = len_corr // 2

#取序列中间值右边的序列（包含中间值）

corr_half = correlation[mid_index:]

#lags = np.arange(-len(s1_new) + 1, len(s1_new)) # Lags array

lags = np.arange(0, len(s1_new)) # Lags array

print("Length of t lags:", len(lags))

# Calculate flow speed using the estimated time delay

# Find the peak of the cross-correlation corresponds to the time delay

delay = lags[np.argmax(corr_half)] # 相位差所对应的信号序列值

# 采样时间

sample_time = (period*T) / len(t_new)

time_delay = delay * sample_time # 两个信号间的延迟时间

phase_shift = (time_delay / T) * 2 * np.pi # 由时间延迟换算成的两个信号序列的相位差

phase_shift_deg = phase_shift * (180 / np.pi) # 由相位差换成的两个信号序列的角度差

print("Ts Delayed cycles:", delay, ", Delayed time: ", time_delay, "degree:", phase_shift_deg) # 将延迟转换为相位差

print("Sample time interval:",sample_time)

# 计算所得的流速

v_estimated = (math.sqrt((L**2)+(time_delay**2)*(c**2))-L)/(time_delay * math.sin(theta))

print('Estimated velocity: ', v_estimated)

# 输出图

fig, (ax_origin, ax_interpo, ax_corr) = plt.subplots(3, 1, figsize=(12, 8))

# 原始信号图

ax_origin.plot(t, s0, label='Signal 1')

ax_origin.plot(t, s1, label='Signal 2')

ax_origin.set_title('Original signals')

ax_origin.legend()

# 插值后的信号图

ax_interpo.plot(t_new, s0_new, label='Signal 1')

ax_interpo.plot(t_new, s1_new, label='Signal 2')

ax_interpo.set_title('interpolated signals')

ax_interpo.legend()

# 互相关图

ax_corr.plot(correlation)

ax_corr.axvline(x = len(correlation)//2 + delay, color = 'r', linestyle = '--', label = "Max correlation at delay")

ax_corr.set_title('Cross-correlation between signal 1 and signal 2')

ax_corr.legend()

plt.tight_layout()

plt.show()

return

except Exception as e:

print("Error:",e)

if __name__=='__main__':

cor_demo()

发送到邮箱 |
+1 赞 0
收藏
评论 0
| 转发至：

本文由FY转载自AMPHENOL SENSORS（安费诺传感器学堂公众号），原文标题为:流量传感器（2-1）超声流量传感器-信号采样率的影响及相关处理插值模拟部分的代码更新，本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。

全部评论（0）

暂无评论

流量传感器（2）超声流量传感器—相位差和信号相关性原理

之前我们简单介绍了基于差压的流量传感器，这次我们要开始基于超声的流量计。超声流量计是一种测量液体或气体流量的仪器，其工作原理基于超声波在介质中传播的特性。这种流量计可以在无需接触或干扰流体本身的情况下进行测量，因此被广泛应用于各种工业环境，尤其是在需要无接触或无损测量的场合。

设计经验发布时间 : 2024-06-18

研讨会2024年世强硬创新技术研讨会：IC、元件、材料、电气、电机、国产化等最新产品与前沿技术

立即报名并查看日程！世强硬创新技术研讨会联合全球1000家顶级原厂发布2024最前沿技术、最新产品以及解决方案，助力硬件企业工程师快速了解市场新品动态，点燃创意火花，加速研发项目进度。

活动发布时间 : 2023-10-24

流量传感器（1）差压式流量传感器

流量传感器是一种用于测量流体在一定时间内通过一定横截面的量（流量）的设备，根据测量原理不同，可以分为但不仅限于以下几种类型：差压式流量传感器，涡街流量传感器，磁电式流量传感器，超声波流量传感器，质量流量计。本文主要介绍差压式流量传感器。

技术探讨发布时间 : 2024-06-07

AASCAFS3000 MEMS 质量流量传感器

型号- AASCAFS300,CAFS3000,AASCAFS3000,AASCAFS300□-□-□

数据手册 - AMPHENOL SENSORS - 01/2018 PDF 中文下载

【应用】安费诺压力传感器NPP-301B-200AT用于风淋设备中，测量压力范围达200kpa

安费诺推出的NPP-301B-200AT是一款测量压力范围200kpa的压力感应单元，风淋设备上的压力传感器的需求量程一般为0-130kpa，该传感器是一个SO-8封装压力前端感应单元。

应用方案发布时间 : 2022-05-19

【产品】专为排放控制和电机管理设计的LMS空气质量流量传感器

I2S（安费诺子厂牌）LMS空气质量流量传感器是专门为测量与车辆排放和电机控制相关的空气量而开发的。根据热膜风速计的测量原理，质量空气流量传感器由成对布置的温度传感器和加热器组成。其紧凑的设计带有法兰安装件，不仅可以轻松集成到流道（管道）中，而且还可以确保在各种系统中灵活安装。LMS也可以选择配备温度传感器，用于额外测量介质温度。

新产品发布时间 : 2020-01-22

Amphenol Sensors(安费诺)/Thermometrics 温度传感器选型指南

目录- 温度传感器产品介绍及应用领域 NTC热敏电阻/PTC热敏电阻探针和组件其他技术和附件

型号- T5D,HM,YA,YB,YC,P60,YD,YF,P65,YG,YH,RL40,YK,YL,YP,YR,EC95,GC32,YS,RL45,GC16,B35,UD20,RL30,3006,AB6,MELF,JA,YS4019,JB,JTC,JC,JD,RL35,JE,JF,MF65,SP85,JS2945,JI,B43,JL,JM,JP,FP10,JR,JTR,CTR100,FP14,P85,JW,M,NDK,T,NDM,CTR65,NDL,ZTP,BB07,PT1000,0706,BB05,NDP,YS4020,NDU,YSM 4021,CL,CTR85,BR16,KU,BR14,KY,BR11,TC,FP07,1403,NHQM,YSM,TH,R100,TM,MA400,PTSM,TP,1803,BB11,EVAP,P100,MA100,DK,SC30,R60,BR23,P20,R65,HVAC,P25,YM120,PT200,EVAPA1450,MS,DKM,MT,CTR60,P30,RL1004,BR32,A1447-A1450,ND,PTA,NK,EVAPA1447,1703,PTE,PTD,SP100,PTF,DC95,PTH,B05,B07,PTO,EVAP A1424,SC50,R85,BR42,C100,2006,JYA,NHQ,NHQMM,GC11,GC14,GE,RL20,M2000,B10,PT100,B14,GT,BR55,MC65,SP60,TK95,SP65,RL14,RL060628,RL10

选型指南 - AMPHENOL SENSORS PDF 中文下载

Amphenol Sensors(安费诺)温度传感器/MEMS压力传感器/C〇2、湿度、灰尘传感器选型指南

目录- Sensors Temperature Sensors Pressure Sensors CO2, Humidity & Dust Sensors

型号- DK SERIES,NDP SERIES,NHQ SERIES,AAS-AQS-UNO-RH-CO2,RL40,T5D SERIES,FMA SERIES,GC32,EC95,AB6 SERIES,RL45,GC16,GT SERIES,DKM SERIES,CTP65,M SERIES,UD20,S SERIES,CTP60,RL30,AIT SERIES,GE-1935,TH SERIES,NDL SERIES,3006,MELF,YS4019,RL35,HM SERIES,GE-2102,GE-2103,JS2945,T6715,T6613-X,AAS-AQS-UNO,TM SERIES,R85 SERIES,SM-UART-04L,YSM SERIES,FP10,NPI-15,T6715-X,FP14,NPC-120,HS12SP,NPI-19,B35 SERIES,T6713,BB07,SUF SERIES,NK SERIES,BB05,YS4020,T6703,YSM 4021,YR SERIES,BR16,A-1737,BR14,T6700,BR11,T SERIES,FP07,1403,NHQM,P85 SERIES,ZTP SERIES,JF SERIES,NDK SERIES,JS8741,NPH SERIES,JS8746,R100,JR SERIES,PTSM,MA400,SM-PWM-01C,JB SERIES,1803,BB11,B05 SERIES,T6616,EVAP,YF SERIES,JA SERIES,P100,YD SERIES,YH SERIES,MF65 SERIES,YG SERIES,MA100,JIC SERIES,YB SERIES,B43 SERIES,T9602,NPC-100,YA SERIES,YC SERIES,SC30,CTP100,BR23,T6613,PTD SERIES,PTE SERIES,YM120,HVAC,JTC SERIES,JTR SERIES,MS SERIES,YK SERIES,WTF083B001,P30 SERIES,YL SERIES,YP SERIES,PTA SERIES,PTH SERIES,ND SERIES,B07 SERIES,PTF SERIES,PTO SERIES,P60 SERIES,JM SERIES,YS SERIES,T6600,RL1004,BR32,JS6780,JI SERIES,HS30P,JW SERIES,A1447-A1450,JS SERIES,TP SERIES,JE SERIES,JC SERIES,GE-1856,1703,B14 SERIES,T6615-X,GE SERIES,R65 SERIES,DC95,JYA SERIES,T3000,EVAP A1424,SC50,BR42,A-1266,C100,GE-1923,NPP-301,706 SERIES,2006,NKA SERIES,AS SERIES,B10 SERIES,P25 SERIES,NHQMM,GC11,RL20,CL SERIES,P20 SERIES,GC14,GE-1920,NPC-1220,JP SERIES,P65 SERIES,ES SERIES,CTP85,T6713-X SERIES,BR55,MC65,KU SERIES,TK95,NDM SERIES,R60 SERIES,NDU SERIES,NPC-1210,TC SERIES,JL SERIES,RL14,JD SERIES,RL060628,RL10

选型指南 - AMPHENOL SENSORS - 05/2019 PDF 英文下载

MEMS流量传感器的工作原理、应用

流量传感器是检测液体、气体和其他物质的速度和流速的传感器，检测方法有接触式和非接触式两种。

技术探讨发布时间 : 2024-09-20

Amphenol Sensors(安费诺)/All Sensors 压力传感器选型指南（简版）

目录- 传感器解决方案及产品优势介绍传感器技术介绍单芯片压力传感器双芯电路交叉耦合补偿压力传感器双芯电路和气路交叉耦合补偿压力传感器传感器应用领域介绍压力单位换算传感器通用名词解释

型号- DLH,ADCX,ACPC-C,AXCA,ACPC,BLV,DLV,ACPC-H,AXCA-PRIME,AXCA-MIDDLE,MAMP,MLV,SAMP,ACPC-P,BLC,ADUX,BLVR,MAMP-/P,ADCA,DLH,DLVR,DLVR,BLCR,MAMP-P,MDCX,ADO,BLV,AXCX-PRIME-INCH,DLHR,DLHR,AXCX,MLV,AXCA-MIL,BLC,DLC,ADO-MIL

选型指南 - AMPHENOL SENSORS PDF 中文下载

Amphenol Sensors（安费诺）建筑及工业应用传感器选型指南

目录- Chip Cap 2完全校准的温湿度传感器 Telaire Ventostat®T8700壁挂式温湿度变送器 Telaire Ventostat®T8031 CO2小型风管式C02传感器 Telaire®T8041/T8042 分管式C02传感器 Telaire T8100-R系列挂壁式C02和温度变送器（带继电器） Telaire®7000室内空气品质监测器 Telaire VaporstatTM 9002红外露点变送器 Telaire®配件 Telaire HumiTrac™温湿度变送器 T9602湿度与温度传感器 AAS-53系列水管型温度变送器 ADT/AOT/AIT温湿度变送器使用说明书

型号- P40250128,CC2D265,P40250129,P40250126,P40250127,P40250125,P40250122,P40250123,DC95F302W,P40250120,P40250121,T8031,CC2D255,EHR-4,T8100-D-R,P40250139,K53,T8700,CC2A23,PT1000A,AIT,PT1000B,CC2A25,P40250133,P40250131,T2075NG,P40250130,T804K0-10V,T1508,T8200-D-5P,T8042-5VI0-5V,T9602-5-A-1,NI1000,9002,T9602-3-A-1,T5100,P40250149,CC2A35,T8700-E-D,P40250147,0-5000PPM,P40250144,PT100A,T7001I,P40250145,PT100B,P40250142,P40250143,T8100,S4B-EH,CC2A33,P40250141,CC2D235,CC2D355,T7001,PT1000,T2072,T7001D,CC2D25,T9602-3-A,T8042I0-10V,CC2D23,P40250156,T8041,T8100-R,P40250151,T8042,P40250150,T9602-3-D,NTC10K,CC2025,7000,T9602-3-D-1,CC2D35,T9602,CC2D33,ADT,NTC15K,T8200,CC2D335,CHIPCAP 2,NTC10K-II,T2090,T1551,T1552,MPNT3D03750M4,NTC20K,T2007,T8700-D,T8700-E,T8100,T2080,T8100-EC,P40250109,PA0250118,T8100-E-D-GN-5P-R,PA0250115,T1505,P40254275,P40254276,P40254277,P40250189,P40250186,P40250184,P40250185,T8300,P40250182,P40250183,P40250181,AAS-53,8000,PT100,T7001SK,P40250119,NTC10K-A,AOT,P40250117,T9602-5-A,P40250113,P40250114,P40250111,P40250112,DC95F103W,T2076NG,P40250110,P40250193,T9602-5-D,T8001,P40250191,7001D,P40250192,T8002,T9602-5-D-1,MPNV12R30M 16004616,B4B-EH-A,P40250190,T8041-5VI0-5V,RS485,NTC10K-III

选型指南 - AMPHENOL SENSORS PDF 中文下载

美蓓亚流量传感器：从精密检测到智能应用的科技桥梁

在这个万物互联的时代，流量传感器作为感知世界的“眼睛”，正默默地在各个领域发挥着重要作用。它不仅能够准确测量液体、气体等物质的流速，还以其独特的检测方式-―接触式与非接触式，满足不同场景的需求，接触式传感器以高精度著称，而非接触式则凭借其安装便捷性赢得青睐。

产品发布时间 : 2024-09-14

Amphenol Sensors(安费诺) 汽车传感器选型指南

目录- 汽车传感器解决方案介绍车厢空气质量系列传感器排放处理系列传感器新能源汽车传感器应用测量汽车应用中最为关键的参数

型号- SM-UART-01L,PT200,T6703,TPMS,DPS,G-CAP2,SM-UART-01D,A2103,NPI-19,T6713,A-2102,EGR,A-2103,NPP-301,GE-1935,A-2121,ZTP,DPF,SM-UART-01L+,SM-PWM-01C,NPX1

选型指南 - AMPHENOL SENSORS PDF 中文下载

Amphenol Sensors(安费诺) 医疗传感器选型指南

目录- NPA贴片式压力传感器系列 NTC AB6 型 "SC/MC"系列专为医疗设汁 MA100系列 ZTP-148SR系列 ZTP-101T系列 NPC-100系列一次性医疗压力传感器 NPC-1210系列 NPG-1220系列中压传感器 NPI-12卫生型压力传感器、不锈钢介质隔离压力传感器 NPI-15系列电流激励高压、介质隔离压力传感器 NPI-15VC系列电压激励、高压、介质隔离压力传感器 NPI-19系列电流激励、中压、介质隔离压力传感器 NPI-19系列电压激励、中压、介质隔离压力传感器 NPP-301系列贴片封装压力传感器

型号- NPP-301B-700AT,NPC-1001000,NPI-12-101G,MC65F103C,NPP-301A-100AT,NPI-19X-YYYZZ,NPI-15X-YYYZZ,NPI-19J-XXX,B35,ZTP-148SR,NPI-19A-XXX,MC65F103A,NPP-301A-200A,MC65F103B,AB6,NPA-300,NPI-19H-XXX,NPA-700,AB6E8,B43,NPP-301B-200A,NPI-12,NPI-19X-XXXXV,NPI-15,SC30F103W,NPP系列,NPP-301B-200AT,SC30F103V,MA100BF103C,NPI-19,SC30F103A,SC,MA100BF103B,MA100BF103A,NPI-15B-XXX,MA100GG232C,NPI-15C-C00903,NNP301B,NNP301A,MA100GG103CN,NPP-301B-700A,BR16,BR14,BR11,NPC-1210XXXX-YZ,ZTP-101T,NPC-100T,MA100GG103BN,MA100,NPP-301A-100A,NPC-100,NPI-19A-C01864,BR23,P20,P25,AB6B4,MC65F232A,MC,AB6B2,MC系列,NPI-19A-002GV,MA100GG103AN,AB6A8-BR16KA103N,NPI-15VC,NPP-301A-200AT,P30,BR32,NPA-100,NPC-1220XXXX-YZ,NPA-500,SC50F103W,NPP-301B-100A,NPA,NPP-301B-100AT,MC65F502B,NPI-15A-XXX,B05,B07,SC30Y103W,NPI-15J-XXX,NPP,NPP-301A-700A,BR42,NPP-301,MA100GG103B,NPI-19B-XXX,NPI-12-101GH,MA100GG103A,MC65G503B,MA100GG103C,NPC-1220,NPP-301A-700AT,B10,NPI-15H-XXX,B14,NPI-15XXXXXX,NTC AB6,BR55,NPC-1210,SC系列

选型指南 - AMPHENOL SENSORS - 2018年7月 PDF 中文下载