数字滤波器(6)—FIR频域连续滤波“重叠相加法”C++源码
[编者按]传感器和信号处理仅一线之隔，信号的前后端合理搭配，是我们更准确地感知这个世界的一种基本态度和方式。
FIR频域重叠相加法
还记得我们（此处有重复之嫌）之前的发文《FIR连续采样分段卷积时域重叠相加法》？不过那是在时域处理的模拟和仿真。这次我们的内容是用C++在频域实现的滤波卷积法，仍然是重叠相加法，届时大家可以比较一下两种方式的差异。
基本是通过两个处理过程。
（1）频域的重叠相加法示意图再拿来用一下。如下图所示[1]。
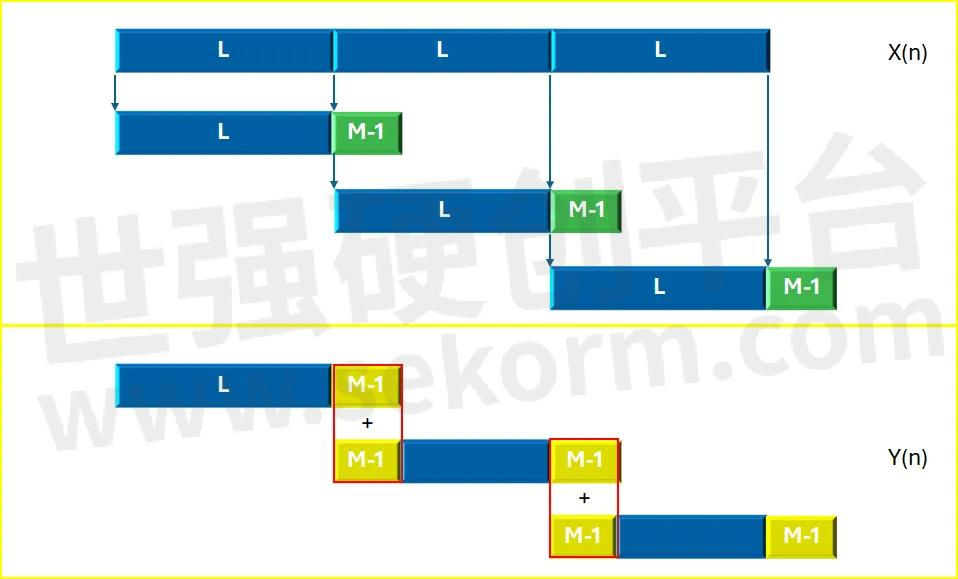
（2）再借用一下的时域卷积经傅里叶FFT变换后，在频域成为对应的相乘；然后再通过IFFT将中间结果转换回时域时序结果。
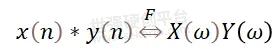
让我们直接跳进话题，先看模拟测试结果，后看C++源码。
模拟情节设定
50Hz选频滤波，信号中混有110Hz和210H在的干扰信号和幅值为1的直流DC。
模拟信号及其频谱的输出请查看我们前面的文章。这里的代码只提供将模拟信号进行了频域重叠相加处理，生成的滤波前后模拟信号和被滤波处理后的数据波形的比较（见下图）。
还记得我们（此处重复）之前用C++来模拟时域处理的滤波模拟程序吗？
你又猜对了，又是那个滤波器，又被用上了！但，是不同的实现处理方式。
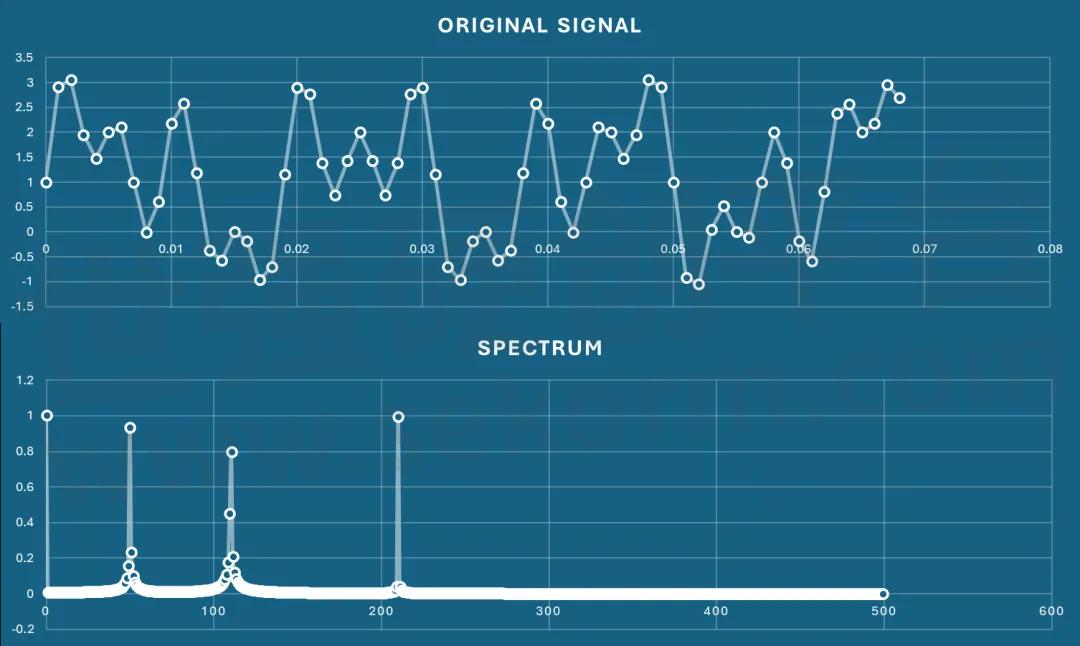
滤波处理之前的波形和频谱图
滤波之后，直流和其他频率的信号已经不见，只留下50Hz的正弦波（见下图）。
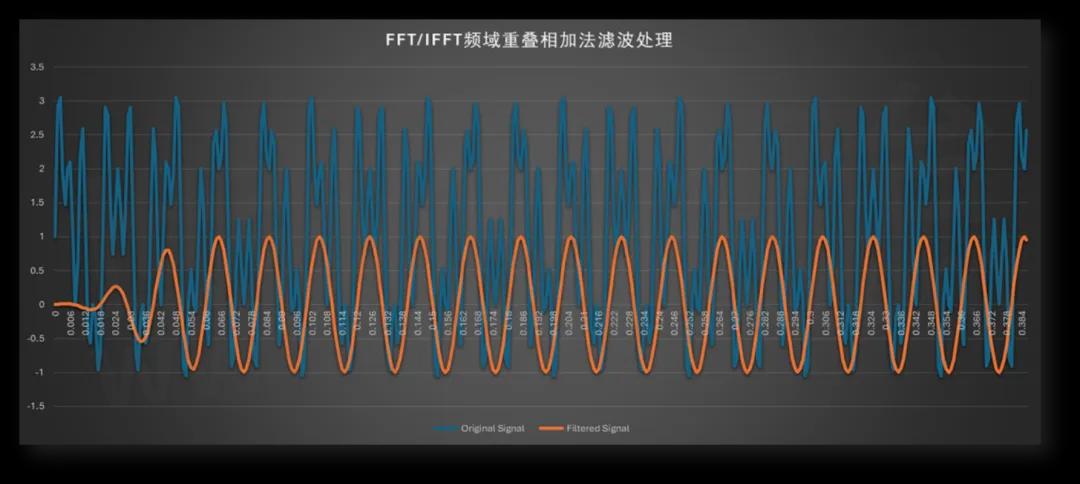
频域重叠相加滤波前后的波形比较
图由csv文件处理后生成。又见此图，是不是有熟悉的感觉？
频域连续滤波模拟和验证C++源码
/*
Project Name: Demonstration & Validation for signal filtering via the
"Overlap-Add" method implemented through FFT/IFFT based on Fast Fourier Transform (FFT)
based on the Cooley-Tukey algorithm.
Copyright (c) 2024 Amphenol Sensors
Author: L.L.
This software is provided 'as-is', without any express or implied
warranty and for simulation/demostration purpose. In no event will the authors be held liable for any damages
arising from the use of this software.
Permission is granted to anyone to use this software for any purpose,
including commercial applications, and to alter it and redistribute it
freely, subject to the following restrictions:
The origin of this software must not be misrepresented; you must not
claim that you wrote the original software. If you use this software
in a product, an acknowledgment in the product documentation would be
appreciated but is not required.
*/
#include <complex>
#include <cmath>
#include <stdio.h>
#include <iostream>
#include <vector>
#include <fstream>
#include <math.h>
#include <algorithm>
const double PI = 3.1415926535897932384;
const double SAMPLE_RATE = 1000.0; // 1000Hz
const int N = 1024; // 假设采样分段数为1024
using namespace std; // 声明使用std命名空间
#define SEL_FFT 0
#define SEL_IFFT 1
#define SEL_FFTIFFT 2
#define SIM_CYCLE_CNT 3.0
// 模拟信号函数
vector<complex<double>> generateSignal(double sampleRate, double seconds)
{
size_t signal_len = (size_t)(sampleRate * seconds);
vector<complex<double>> signal(signal_len); // 定义模拟信号的数组长度
for (size_t i = 0; i < signal_len; ++i)
{
// 包含50Hz和110Hz,210Hz信号,DC
signal[i].real(1+ sin((2 * PI * (double)i * 50) / sampleRate) + sin((2 * PI * (double)i * 210) / sampleRate) + sin((2 * PI * (double)i * 110) / sampleRate));
signal[i].imag(0);
}
return signal;
}
// 基于Cooley-Tukey算法的FFT
void fft2(vector<complex<double>> &x)
{
size_t n = x.size();
if (n <= 1)
return;
// 把序列分为奇偶两部分
vector<complex<double>> even(n / 2), odd(n / 2);
for (size_t i = 0; 2 * i < n; i++)
{
even[i] = x[i * 2];
odd[i] = x[i * 2 + 1];
}
// 递归解决每一个序列
fft2(even);
fft2(odd);
// 结合步骤
for (size_t i = 0; 2 * i < n; i++)
{
complex<double> t = polar(1.0, -2 * PI * (double)i / (double)n) * odd[i];
x[i] = even[i] + t;
x[i + n / 2] = even[i] - t;
}
}
// 基于Cooley-Tukey算法的IFFT
void ifft2(vector<complex<double>> &x)
{
size_t n = x.size();
if (n <= 1)
return;
vector<complex<double>> even(n / 2), odd(n / 2);
for (size_t i = 0; 2 * i < n; i++)
{
even[i] = x[i * 2];
odd[i] = x[i * 2 + 1];
}
ifft2(even);
ifft2(odd);
for (size_t i = 0; 2 * i < n; i++)
{
complex<double> t = polar(1.0, 2 * PI * (double)i /(double) n) * odd[i];
x[i] = even[i] + t;
x[i + n / 2] = even[i] - t;
}
// 最后除以n
if (n > 1)
{
for (size_t i = 0; i < n; i++)
{
x[i] /= 2;
}
}
}
// 将数据写入文件
void writeToFile(const vector<complex<double>> &Original_signal, const vector<complex<double>> &Proceeded_Signal, const string &filename, int Type_sel)
{
ofstream file(filename);
if (Type_sel==SEL_FFTIFFT)
{
file << "time(s)" << ", " << "Original Signal"<< ", " << "Filtered Signal" << "\n";
for (size_t i = 0; i < Original_signal.size(); i++)
{
file << (double)i / SAMPLE_RATE << ", " <<Original_signal[i].real() << ", "<< Proceeded_Signal[i].real() << "\n";
}
}
file.close();
}
// 测试模拟程序
int main()
{
//FIR filter：50Hz选频FIR滤波器
vector<double> b{0.0010175493084400998, 0.0010954624020866333, 0.001080635650435545, 0.0009293052645812359,
0.0005868808563577278, -8.138309855847798e-19, -0.0008644147524968251, -0.0019966389877814107,
-0.003323586744207458, -0.004696461345361978, -0.005892320462621699, -0.006633249964255378,
-0.006623614506478284, -0.005601944833604465, -0.0034001773970723163, -7.334366341273803e-18,
0.004425290874832446, 0.00949426225087417, 0.014634010415364655, 0.019132982942933127,
0.022226796444847933, 0.023207550009729024, 0.021541722692400025, 0.01697833945185371,
0.009628503914736117, -6.755395515820625e-18, -0.01102370844120733, -0.02226281209657117,
-0.032372473621654914, -0.04001099412924139, -0.04402269970024527, -0.043609484958132556,
-0.03846490807520255, -0.028848803480728435, -0.015588116829396594, -9.10410551538968e-18,
0.016255406162706088, 0.031374390998733945, 0.04363491329762711, 0.051616779739690075,
0.05438594145724075, 0.051616779739690075, 0.04363491329762711, 0.031374390998733945,
0.016255406162706088, -9.10410551538968e-18, -0.015588116829396594, -0.028848803480728435,
-0.03846490807520255, -0.043609484958132556, -0.04402269970024527, -0.0400109941292414,
-0.032372473621654914, -0.022262812096571168, -0.01102370844120733, -6.755395515820627e-18,
0.009628503914736117, 0.016978339451853702, 0.021541722692400025, 0.023207550009729034,
0.022226796444847933, 0.01913298294293312, 0.014634010415364655, 0.009494262250874175,
0.004425290874832446, -7.3343663412738e-18, -0.0034001773970723163, -0.005601944833604469,
-0.006623614506478284, -0.006633249964255374, -0.005892320462621699, -0.00469646134536198,
-0.003323586744207458, -0.001996638987781409, -0.0008644147524968251, -8.138309855847805e-19,
0.0005868808563577278, 0.0009293052645812359, 0.001080635650435545, 0.0010954624020866333,
0.0010175493084400998};
// (1) Resize filter coefficients
vector<complex<double>> H(b.size());
for(size_t i=0; i< b.size(); i++)
{
H[i] = complex<double>(b[i],0);
}
H.resize(N, complex<double>(0.0, 0.0));
// (2)Generate simulation data sequences
size_t DataSeg_len_L = N - b.size() + 1; // Data segmeng Length = L
double daq_duration = (double)DataSeg_len_L * SIM_CYCLE_CNT / SAMPLE_RATE;
vector<complex<double>>Original_signal = generateSignal(SAMPLE_RATE, daq_duration); // Generate data sequence, L * 3
// (3-1) Define a 2-D vector，3 columns, to simulate DAQ and filtering process for 3 rounds
vector<vector<complex<double>>> seg_Dates(3);
// (3-2) Initialize data segment
for (size_t i = 0; i < seg_Dates.size(); i++)
{
seg_Dates[i].resize(DataSeg_len_L,complex<double>(0.0, 0.0));
// devide Original_signal into 3 parts to simulate consequent DAQ for 3 cycles
for(size_t j=0; j<DataSeg_len_L;j++)
{
seg_Dates[i][j] = Original_signal[i * DataSeg_len_L + j];
}
seg_Dates[i].resize(N, complex<double>(0.0, 0.0)); // resize each data segment to N = L + M - 1
}
// (4) Start to FFT/IFFT and generate involution result
vector<complex<double>> Filtered_signal(DataSeg_len_L * (size_t)(SIM_CYCLE_CNT) + b.size() -1 ); //L * 3 + (M - 1)
fft2(H);
// (4-1) Simulate 3 cycles of involution: L * 3
for(size_t i=0; i< seg_Dates.size(); i++)
{
fft2(seg_Dates[i]);
for(size_t j = 0; j< seg_Dates[i].size(); j++)
{
seg_Dates[i][j] = seg_Dates[i][j] * H[j];
}
ifft2(seg_Dates[i]);
for(size_t k = 0; k< seg_Dates[i].size(); k++)
{
Filtered_signal[i*DataSeg_len_L + k] += seg_Dates[i][k];
}
}
// (5) Save Origianl signal & result (data after filtering) into csv file
writeToFile(Original_signal, Filtered_signal,"output_Filtered2.csv", SEL_FFTIFFT);
return 0;
}
时间仓促，有些功能和细节并没有考虑太多，这里功能验证是第一。
FFT/IFFT是基于库里-图基的算法，各位可以选用其他的来优化替代；
有些参数可以单独变，有些参数却是关联的。
[1]《数字信号处理—原理、算法与应用》，第四版，普鲁克斯著，方艳梅等译，北京电子工业出版社，2014.8
- |
- +1 赞 0
- 收藏
- 评论 0
本文由赵优秀转载自AMPHENOL SENSORS 微信公众号，原文标题为:数字滤波器(6)—FIR频域连续滤波“重叠相加法”C++源码，本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。
相关研发服务和供应服务
相关推荐
【经验】SGX传感器技术电化学气体传感器用电子电路的设计提供指导
本文为Amphenol Sensors旗下SGX传感器技术电化学气体传感器的电子电路设计提供指导。
设计经验 发布时间 : 2019-09-21
【经验】一文介绍清楚一次性有创性血压传感器的使用和特点、以及对压力传感的要求
笔者Amphenol Sensors的工程师，本文将对一次性有创性血压传感器的使用及特点，结合国内的医药行业对血压传感器的标准，做一个简单的性能指标上的解说。
设计经验 发布时间 : 2020-03-31
数字滤波器C语言的模拟及验证
本文通过一个带通滤波器的Python验证，再转换到C++代码模拟验证的实现过程说明数字滤波器是如何工作的。我们先通过Python测试验证，并生成滤波器的参数数据。然后将获取的参数用到C程序中重现滤波器。
设计经验 发布时间 : 2024-06-29
Amphenol Sensors(安费诺)/Thermometrics 温度传感器选型指南
目录- 温度传感器产品介绍及应用领域 NTC热敏电阻/PTC热敏电阻 探针和组件 其他技术和附件
型号- T5D,HM,YA,YB,YC,P60,YD,YF,P65,YG,YH,RL40,YK,YL,YP,YR,EC95,GC32,YS,RL45,GC16,B35,UD20,RL30,3006,AB6,MELF,JA,YS4019,JB,JTC,JC,JD,RL35,JE,JF,MF65,SP85,JS2945,JI,B43,JL,JM,JP,FP10,JR,JTR,CTR100,FP14,P85,JW,M,NDK,T,NDM,CTR65,NDL,ZTP,BB07,PT1000,0706,BB05,NDP,YS4020,NDU,YSM 4021,CL,CTR85,BR16,KU,BR14,KY,BR11,TC,FP07,1403,NHQM,YSM,TH,R100,TM,MA400,PTSM,TP,1803,BB11,EVAP,P100,MA100,DK,SC30,R60,BR23,P20,R65,HVAC,P25,YM120,PT200,EVAPA1450,MS,DKM,MT,CTR60,P30,RL1004,BR32,A1447-A1450,ND,PTA,NK,EVAPA1447,1703,PTE,PTD,SP100,PTF,DC95,PTH,B05,B07,PTO,EVAP A1424,SC50,R85,BR42,C100,2006,JYA,NHQ,NHQMM,GC11,GC14,GE,RL20,M2000,B10,PT100,B14,GT,BR55,MC65,SP60,TK95,SP65,RL14,RL060628,RL10
Amphenol Sensors(安费诺)温度传感器/MEMS压力传感器/C〇2、湿度、灰尘传感器选型指南
目录- Sensors Temperature Sensors Pressure Sensors CO2, Humidity & Dust Sensors
型号- DK SERIES,NDP SERIES,NHQ SERIES,AAS-AQS-UNO-RH-CO2,RL40,T5D SERIES,FMA SERIES,GC32,EC95,AB6 SERIES,RL45,GC16,GT SERIES,DKM SERIES,CTP65,M SERIES,UD20,S SERIES,CTP60,RL30,AIT SERIES,GE-1935,TH SERIES,NDL SERIES,3006,MELF,YS4019,RL35,HM SERIES,GE-2102,GE-2103,JS2945,T6715,T6613-X,AAS-AQS-UNO,TM SERIES,R85 SERIES,SM-UART-04L,YSM SERIES,FP10,NPI-15,T6715-X,FP14,NPC-120,HS12SP,NPI-19,B35 SERIES,T6713,BB07,SUF SERIES,NK SERIES,BB05,YS4020,T6703,YSM 4021,YR SERIES,BR16,A-1737,BR14,T6700,BR11,T SERIES,FP07,1403,NHQM,P85 SERIES,ZTP SERIES,JF SERIES,NDK SERIES,JS8741,NPH SERIES,JS8746,R100,JR SERIES,PTSM,MA400,SM-PWM-01C,JB SERIES,1803,BB11,B05 SERIES,T6616,EVAP,YF SERIES,JA SERIES,P100,YD SERIES,YH SERIES,MF65 SERIES,YG SERIES,MA100,JIC SERIES,YB SERIES,B43 SERIES,T9602,NPC-100,YA SERIES,YC SERIES,SC30,CTP100,BR23,T6613,PTD SERIES,PTE SERIES,YM120,HVAC,JTC SERIES,JTR SERIES,MS SERIES,YK SERIES,WTF083B001,P30 SERIES,YL SERIES,YP SERIES,PTA SERIES,PTH SERIES,ND SERIES,B07 SERIES,PTF SERIES,PTO SERIES,P60 SERIES,JM SERIES,YS SERIES,T6600,RL1004,BR32,JS6780,JI SERIES,HS30P,JW SERIES,A1447-A1450,JS SERIES,TP SERIES,JE SERIES,JC SERIES,GE-1856,1703,B14 SERIES,T6615-X,GE SERIES,R65 SERIES,DC95,JYA SERIES,T3000,EVAP A1424,SC50,BR42,A-1266,C100,GE-1923,NPP-301,706 SERIES,2006,NKA SERIES,AS SERIES,B10 SERIES,P25 SERIES,NHQMM,GC11,RL20,CL SERIES,P20 SERIES,GC14,GE-1920,NPC-1220,JP SERIES,P65 SERIES,ES SERIES,CTP85,T6713-X SERIES,BR55,MC65,KU SERIES,TK95,NDM SERIES,R60 SERIES,NDU SERIES,NPC-1210,TC SERIES,JL SERIES,RL14,JD SERIES,RL060628,RL10
数字滤波器（4）—IIR/FIR系统对连续采集数据的滤波处理和模拟仿真
在之前我们的博文中，所提到的数据的滤波处理和仿真分析，其实都是围着一段固定长度的模拟数据展开的，除了知道滤波器的幅频、相频响应特性之外，也直观地看到了滤波的效果会是怎么样的。实际应用会怎么样？需要怎么处理？
技术探讨 发布时间 : 2024-08-27
Amphenol Sensors(安费诺)/All Sensors 压力传感器选型指南（简版）
目录- 传感器解决方案及产品优势介绍 传感器技术介绍 单芯片压力传感器 双芯电路交叉耦合补偿压力传感器 双芯电路和气路交叉耦合补偿压力传感器 传感器应用领域介绍 压力单位换算 传感器通用名词解释
型号- DLH,ADCX,ACPC-C,AXCA,ACPC,BLV,DLV,ACPC-H,AXCA-PRIME,AXCA-MIDDLE,MAMP,MLV,SAMP,ACPC-P,BLC,ADUX,BLVR,MAMP-/P,ADCA,DLH,DLVR,DLVR,BLCR,MAMP-P,MDCX,ADO,BLV,AXCX-PRIME-INCH,DLHR,DLHR,AXCX,MLV,AXCA-MIL,BLC,DLC,ADO-MIL
Amphenol Sensors（安费诺）建筑及工业应用传感器选型指南
目录- Chip Cap 2完全校准的温湿度传感器 Telaire Ventostat®T8700壁挂式温湿度变送器 Telaire Ventostat®T8031 CO2小型风管式C02传感器 Telaire®T8041/T8042 分管式C02传感器 Telaire T8100-R系列挂壁式C02和温度变送器（带继电器） Telaire®7000室内空气品质监测器 Telaire VaporstatTM 9002红外露点变送器 Telaire®配件 Telaire HumiTrac™温湿度变送器 T9602湿度与温度传感器 AAS-53系列水管型温度变送器 ADT/AOT/AIT温湿度变送器使用说明书
型号- P40250128,CC2D265,P40250129,P40250126,P40250127,P40250125,P40250122,P40250123,DC95F302W,P40250120,P40250121,T8031,CC2D255,EHR-4,T8100-D-R,P40250139,K53,T8700,CC2A23,PT1000A,AIT,PT1000B,CC2A25,P40250133,P40250131,T2075NG,P40250130,T804K0-10V,T1508,T8200-D-5P,T8042-5VI0-5V,T9602-5-A-1,NI1000,9002,T9602-3-A-1,T5100,P40250149,CC2A35,T8700-E-D,P40250147,0-5000PPM,P40250144,PT100A,T7001I,P40250145,PT100B,P40250142,P40250143,T8100,S4B-EH,CC2A33,P40250141,CC2D235,CC2D355,T7001,PT1000,T2072,T7001D,CC2D25,T9602-3-A,T8042I0-10V,CC2D23,P40250156,T8041,T8100-R,P40250151,T8042,P40250150,T9602-3-D,NTC10K,CC2025,7000,T9602-3-D-1,CC2D35,T9602,CC2D33,ADT,NTC15K,T8200,CC2D335,CHIPCAP 2,NTC10K-II,T2090,T1551,T1552,MPNT3D03750M4,NTC20K,T2007,T8700-D,T8700-E,T8100,T2080,T8100-EC,P40250109,PA0250118,T8100-E-D-GN-5P-R,PA0250115,T1505,P40254275,P40254276,P40254277,P40250189,P40250186,P40250184,P40250185,T8300,P40250182,P40250183,P40250181,AAS-53,8000,PT100,T7001SK,P40250119,NTC10K-A,AOT,P40250117,T9602-5-A,P40250113,P40250114,P40250111,P40250112,DC95F103W,T2076NG,P40250110,P40250193,T9602-5-D,T8001,P40250191,7001D,P40250192,T8002,T9602-5-D-1,MPNV12R30M 16004616,B4B-EH-A,P40250190,T8041-5VI0-5V,RS485,NTC10K-III
数字滤波器（5）—FIR连续采样分段卷积时域重叠相加法
我们提到了FIR系统在时域的分段卷积中使用“重叠保留（Overlap-Save）”的处理方式，这里我们说明一下“重叠相加（Overlap-Add）”的处理方式。
技术探讨 发布时间 : 2024-08-27
AMPHENOL SENSORS（安费诺）温度传感器选型表
AMPHENOL SENSORS（安费诺）温度传感器选型表。25°C 时阻值：5Ω~1.3MΩ，B25/85：2983K~4793K。
|
产品型号
|
品类
|
安装类型
|
封装/外壳
|
25°C 时阻值(Ω)
|
长度-引线(inch、mm)
|
工作温度(℃)
|
电阻容差
|
B25/85
|
|
AL03006-5818-97-G1
|
温度传感器
|
通孔
|
DO-204AH，DO-35，轴向
|
10k
|
1.15"（29.20mm）
|
-50°C ~ 204°C
|
±10%
|
3992K
|
选型表 - AMPHENOL SENSORS 立即选型
Amphenol Sensors(安费诺) 汽车传感器选型指南
目录- 汽车传感器解决方案介绍 车厢空气质量系列传感器 排放处理系列传感器 新能源汽车传感器应用 测量汽车应用中最为关键的参数
型号- SM-UART-01L,PT200,T6703,TPMS,DPS,G-CAP2,SM-UART-01D,A2103,NPI-19,T6713,A-2102,EGR,A-2103,NPP-301,GE-1935,A-2121,ZTP,DPF,SM-UART-01L+,SM-PWM-01C,NPX1
解析数字滤波器（1）——陷波滤波器
有鉴于数字信号处理涉及的面太多，我们必须要把话题收缩。数字滤波的种类也是五花八门，因此再选一个小的类型，AMPHENOL SENSORS将围绕离散线性时不变系统来简单讨论一下陷波滤波器（Notch Filter）和梳状滤波器（Comb Filter），通过代码的演示和输出，我们可以比较一下这两类滤波器的特点。在本文中先以陷波滤波器为题来讨论相关的内容。
技术探讨 发布时间 : 2024-07-25
Amphenol Sensors(安费诺) 医疗传感器选型指南
目录- NPA贴片式压力传感器系列 NTC AB6 型 "SC/MC"系列专为医疗设汁 MA100系列 ZTP-148SR系列 ZTP-101T系列 NPC-100系列一次性医疗压力传感器 NPC-1210系列 NPG-1220系列中压传感器 NPI-12卫生型压力传感器、不锈钢介质隔离压力传感器 NPI-15系列电流激励高压、介质隔离压力传感器 NPI-15VC系列电压激励、高压、介质隔离压力传感器 NPI-19系列电流激励、中压、介质隔离压力传感器 NPI-19系列电压激励、中压、介质隔离压力传感器 NPP-301系列贴片封装压力传感器
型号- NPP-301B-700AT,NPC-1001000,NPI-12-101G,MC65F103C,NPP-301A-100AT,NPI-19X-YYYZZ,NPI-15X-YYYZZ,NPI-19J-XXX,B35,ZTP-148SR,NPI-19A-XXX,MC65F103A,NPP-301A-200A,MC65F103B,AB6,NPA-300,NPI-19H-XXX,NPA-700,AB6E8,B43,NPP-301B-200A,NPI-12,NPI-19X-XXXXV,NPI-15,SC30F103W,NPP系列,NPP-301B-200AT,SC30F103V,MA100BF103C,NPI-19,SC30F103A,SC,MA100BF103B,MA100BF103A,NPI-15B-XXX,MA100GG232C,NPI-15C-C00903,NNP301B,NNP301A,MA100GG103CN,NPP-301B-700A,BR16,BR14,BR11,NPC-1210XXXX-YZ,ZTP-101T,NPC-100T,MA100GG103BN,MA100,NPP-301A-100A,NPC-100,NPI-19A-C01864,BR23,P20,P25,AB6B4,MC65F232A,MC,AB6B2,MC系列,NPI-19A-002GV,MA100GG103AN,AB6A8-BR16KA103N,NPI-15VC,NPP-301A-200AT,P30,BR32,NPA-100,NPC-1220XXXX-YZ,NPA-500,SC50F103W,NPP-301B-100A,NPA,NPP-301B-100AT,MC65F502B,NPI-15A-XXX,B05,B07,SC30Y103W,NPI-15J-XXX,NPP,NPP-301A-700A,BR42,NPP-301,MA100GG103B,NPI-19B-XXX,NPI-12-101GH,MA100GG103A,MC65G503B,MA100GG103C,NPC-1220,NPP-301A-700AT,B10,NPI-15H-XXX,B14,NPI-15XXXXXX,NTC AB6,BR55,NPC-1210,SC系列
解析数字滤波器（2）——梳状滤波器及相关话题
本文AMPHENOL SENSORS将围绕但不限于梳状滤波器进行展开。其中，梳状滤波器，一方面可以滤除特定的频率（尤其是特定频率的谐波），另一方面也可以在信号中对指定频率及其倍频的信号进行拣选。例如图-1所示的滤除指定谐波成分的梳状滤波器的幅频图。
技术探讨 发布时间 : 2024-07-25
电子商城
品牌：AMPHENOL SENSORS
品类：Assembly NTC temperature sensor
价格：￥5.0624
现货： 2,000
品牌：AMPHENOL SENSORS
品类：Surface Mount Pressure Sensors
价格：￥97.5000
现货： 51
品牌：AMPHENOL SENSORS
品类：Air Quality Sensors IR LED Dust Sensor
价格：￥40.5000
现货： 35
品牌：AMPHENOL SENSORS
品类：Board Mount Pressure Sensors
价格：￥253.8839
现货： 30
品牌：AMPHENOL SENSORS
品类：Board Mount Pressure Sensors
价格：￥253.8839
现货： 25
品牌：AMPHENOL SENSORS
品类：Board Mount Pressure Sensors
价格：￥227.5314
现货： 25
品牌：AMPHENOL SENSORS
品类：Low Pressure Compact Sensors
价格：￥125.9778
现货： 25
品牌：AMPHENOL SENSORS
品类：Board Mount Pressure Sensors
价格：￥227.5314
现货： 25
现货市场
品牌：SILICON LABS
品类：Switch Hall Effect Magnetic Position Sensor
价格：￥2.2924
现货：150,000
服务
可定制温度范围-230℃~1150℃、精度可达±0.1°C；支持NTC传感器、PTC传感器、数字式温度传感器、热电堆温度传感器的额定量程和输出/外形尺寸/工作温度范围等参数定制。
提交需求>
可定制板装式压力传感器支持产品量程从5inch水柱到100 psi气压；数字输出压力传感器压力范围0.5~60inH2O，温度补偿范围-20~85ºС；模拟和数字低压传感器可以直接与微控制器通信，具备多种小型SIP和DIP封装可选择。
提交需求>
授权代理品牌：集成电路
授权代理品牌：分立元件
授权代理品牌：接插件及结构件
授权代理品牌：部件、组件及配件
授权代理品牌：电源及模块
授权代理品牌：电子材料
授权代理品牌：仪器仪表及测试配组件
授权代理品牌：电工工具及材料
授权代理品牌：机械电子元件
授权代理品牌：加工与定制
我要提问
登录 | 立即注册
提交评论