数字滤波器（4）—IIR/FIR系统对连续采集数据的滤波处理和模拟仿真

时间： 2024-08-27 来源：Amphenol Sensors（安费诺传感器学堂公众号）

技术问答

选型帮助

研发客服

商务客服

在之前我们的相关数字滤波器博文中，所提到的数据的滤波处理和仿真分析，其实都是围着一段固定长度的模拟数据展开的，除了知道滤波器的幅频、相频响应特性之外，也直观地看到了滤波的效果会是怎么样的。实际应用会怎么样？需要怎么处理？

假设需要对音频，视频，或者储存的大量数据等进行处理时，期待全部读取然后一次处理显然是不合适，也没有必要，而且资源和实时性都无法满足。而分段处理，需要的资源少是一方面，并行和分布处理难道不考虑一下？

那分段处理，能否将每段滤波之后获取的数据直接拼接作为整体滤波后的数据呢？然而分段处理需要考虑有其特殊性。

就信号处理而言，FIR系统和IIR系统的处理方式各有特点。

IIR系统的连续采集滤波

IIR系统的输出不仅依赖于当前和过去的激励输入，而且还依赖于系统过去的输出（反馈）。IIR系统的特性是有无限长的冲击响应，理论上即使停止了前馈输入，它还有系统过去的输出继续作为反馈输入，从而维持输出。如果一定要卷积IIR系统，通常要做适当的截断和近似处理，才可以让IIR滤波的效果在有限的计算资源使用卷积。不过虽然理论可卷，实际多用时域递推的方式。

IIR系统的递推计算，之前我们提供的示例C++滤波器代码中，是为了演示，一次性批发处理多个数据，实际处理是可以根据应用来调整每次输入数据的长度。无论是分段处理还是单个输出，如果保留了过去的输入和输出状态，是可以持续进行处理的。下面是每次输入一个信号x(n)，然后生成/读取一个输出y(n)，一定要正确保留每次的输出和输入。

下面是一个简单IIR单输入滤波的示例，参数没有哈。当然，把这个转换为FIR的滤波处理也是很自然的事情。

#define N 3 // 设置滤波器的阶数

double a[N] = {...}; // 这是滤波器的反馈系数

double b[N] = {...}; // 这是滤波器的前馈系数

double x[N] = {0}; // 这是输入的缓冲数组

double y[N] = {0}; // 这是输出的缓冲数组

double iir_filter(double input)

{

int i;

// 更新输入缓冲数组，循环更替

for (i = N - 1; i > 0; --i)

{

x[i] = x[i - 1];

}

x[0] = input;

// 计算当前的输出

double output = 0;

for (i = 0; i < N; ++i)

{

output += b[i] * x[i] - a[i] * y[i];

}

// 更新输出缓冲数组

for (i = N - 1; i > 0; --i)

{

y[i] = y[i - 1];

}

y[0] = output;

return output;

}

●如果IIR系统长数据分段没有保存过去的状态，我们可以得到下图。

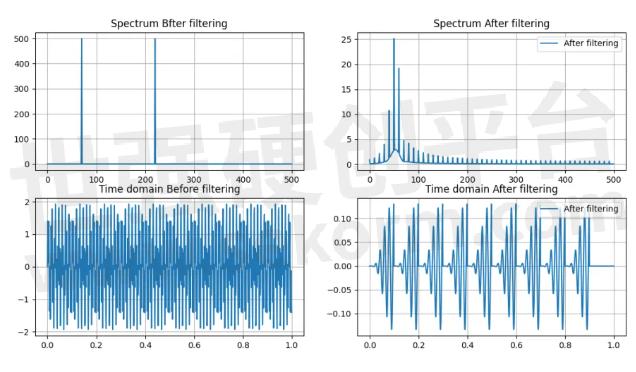
IIR分段滤波没有保留过去的状态

过滤没有处理好，还生成了额外的干扰信号。总之，IIR系统中忘记历史，就会有惩戒啊。

●如果IIR系统长数据分段保存过去的状态，我们可以得到下图：

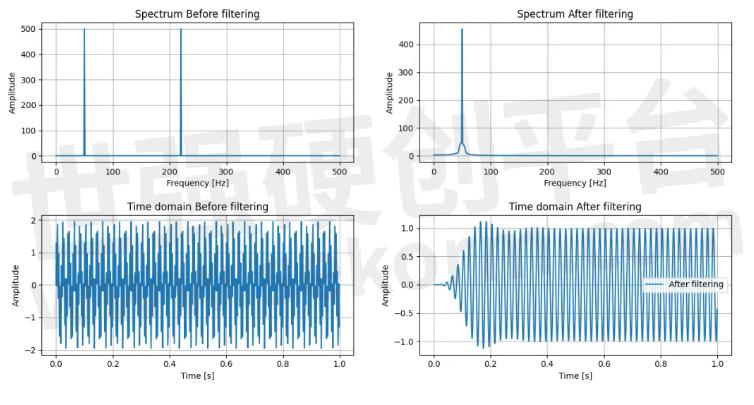
IIR分段滤波有过去的状态

前面两组图相比，差异是不是一目了然？下面是IIR系统每次分段考虑了过去状态的Python模拟代码。

# IIR 系统分段处理：过去状态的处理

import numpy as np

import matplotlib.pyplot as plt

from scipy import signal

from numpy.fft import fft, fftfreq

# 创建模拟信号

# 采样频率

Fs = 1000

nyq = 0.5 * Fs

# 设定阻带频率

low = 45.0

high = 55.0

# 按照通带和阻带频率的顺序来设计滤波器

lowcut = low / nyq

highcut = high / nyq

# 使用iirdesign设计滤波器

b, a = signal.iirdesign([lowcut, highcut], [lowcut - 0.05, highcut + 0.05], gpass=1, gstop=60, ftype='butter', output='ba')

T = 1.0 / Fs # 采样时间间隔

t = np.arange(0, 1, T) # 创建时间轴

x = np.sin(2 * np.pi * 50 * t) + 1 * np.sin(2 * np.pi * 220 * t) # 50Hz和120Hz信号叠加

# 创建一个与x长度相同的用于保存滤波后结果的数组

y = np.zeros_like(x)

# 分段进行滤波

win_size = 100 # 窗口大小

zi = signal.lfilter_zi(b, a) * x[0] # 计算初始状态

for i in range(win_size, len(x)+1, win_size):

y[i-win_size:i], zi = signal.lfilter(b, a, x[i-win_size:i], zi=zi)

# 计算输入信号和输出信号的频谱

frequencies = fftfreq(len(t), 1/Fs)

x_spectrum = np.abs(fft(x))

y_spectrum = np.abs(fft(y))

# 绘制幅频响应图

w, h = signal.freqz(b, a)

plt.figure()

plt.plot(w/(2*np.pi), abs(h))

plt.title('Frequency response')

plt.xlabel('Frequency [Hz]')

plt.ylabel('Gain')

plt.grid()

# 绘制频谱图

plt.figure(figsize=(9, 6))

plt.subplot(221)

plt.title('Spectrum Before filtering')

plt.xlabel('Frequency [Hz]')

plt.ylabel('Amplitude')

plt.grid()

plt.plot(frequencies[:Fs//2], x_spectrum[:Fs//2], label='Before filtering')

plt.subplot(222)

plt.plot(frequencies[:Fs//2], y_spectrum[:Fs//2], label='After filtering')

plt.title('Spectrum After filtering')

plt.xlabel('Frequency [Hz]')

plt.ylabel('Amplitude')

plt.grid()

# 绘制模拟信号和滤波后的信号

plt.subplot(223)

plt.plot(t, x, label='Before filtering')

plt.title('Time domain Before filtering')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid()

plt.subplot(224)

plt.plot(t, y, label='After filtering')

plt.title('Time domain After filtering')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid()

plt.tight_layout()

plt.legend()

plt.show()

FIR系统的连续采集滤波

和IIR系统相比，FIR系统的输出则仅仅依靠当前和过去的输入。但是，要实现相同的滤波效果（不考虑相位线性），FIR往往要更高的阶数才可以完成。阶数越高，意味着越多的资源和越长的系统延迟。

我们知道，FIR滤波器中的每个系数b(n)，都对应于系统的单位冲击响应h(n)。所以，对于FIR滤波器，那我们就可以通过但不限于卷积的方式来处理信号。这里我们围绕卷积的方式来讨论FIR滤波器处理数据分段滤波的两种方法：

●重叠保留(Overlap-Save)

●重叠相加(Overlap-Add)

下面两个等式分别是卷积和FIR滤波处理。

如果把b[k]看作h(k)，则水到渠成，FIR滤波器的处理过程就是一个卷积运算。变成卷积后的另外的好处就是，我们可以利用FFT/IFFT来进行某些大型数据的加速运算——时域的卷积等同于频域的乘积。对于小到中等大小的数组序列，一般也就用时域的卷积了。

但是卷积从现象上看，当我们参与卷积的FIR滤波器长度为M，被卷积的数据序列长度为L，那么，每次卷积的结果的数据序列N长度会是：

N = M + L -1

当你面对每次多出原先数据序列长度L的结果N时？如何取舍？

如果滤波器是从全0的状态开始的，滤波器需要一定的"预热"时间才能达到稳定的工作状态。滤波器的"预热"过程就是滤波器读取前N个样本的过程。因此，你会看到滤波后的数据最开始部分是从0开始，然后逐渐看到正常的输出波形。

另外，我们示例的滤波器是加窗处理的，而且模拟信号频率比较单一，相距也较远，否则，处理不好的滤波结果会让人感觉出乎意外。因为每次截取一段数据，相对于给采集的数据加了一个矩形窗，而我们在设计滤波器时，是需要对这个矩形窗进行额外加窗处理的。矩形窗对于波形而言存在着频谱泄漏和主瓣宽度等问题，对数据的处理有时候会比较麻烦。——注意，要跑题了吧？

我们看模拟结果。下图为待滤波处理的模拟信号。500Hz+1400Hz。

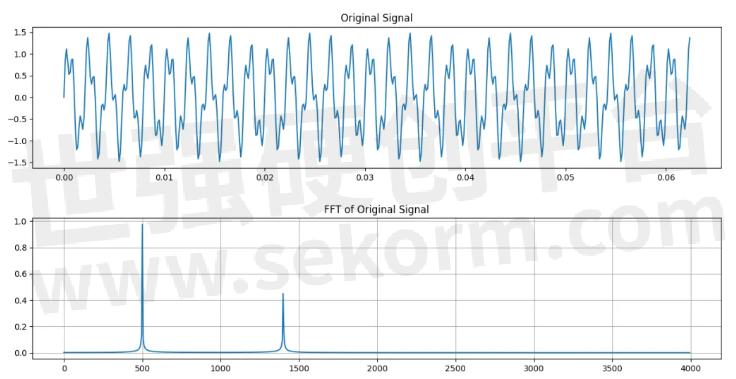
下图为矩形窗滤波器的幅频响应——知道为什么我要选1400Hz作为被滤掉的信号了吧？

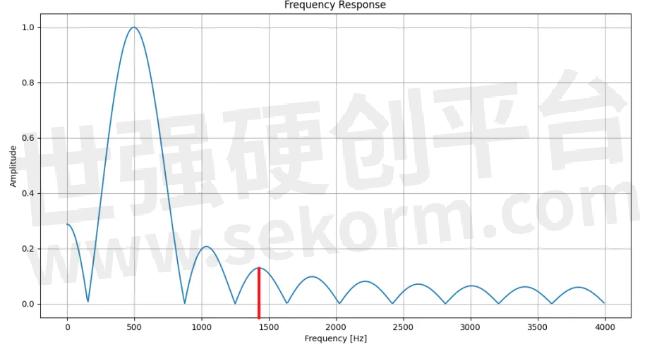
矩形窗选频滤波器幅频特性

这个例子仅仅是为了说明矩形窗的影响。下面是矩形窗滤波器的结果，500Hz+1400Hz的信号经过滤波之后的输出。——跑题十万八千里是为了一扇窗？

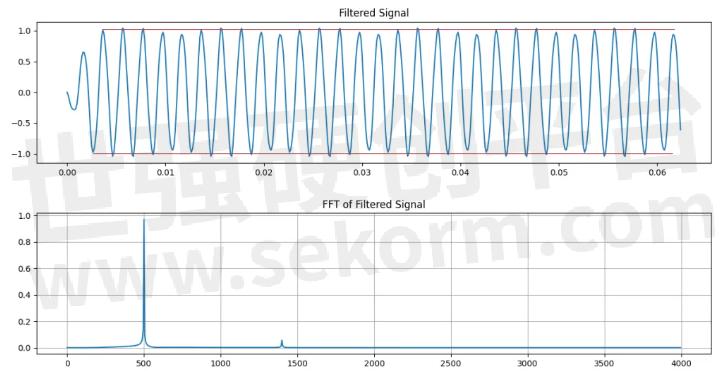
矩形窗滤波器处理结果

而加汉明窗的滤波结果在试验设定条件下则要好一些，同样留意1400Hz处。如下图。

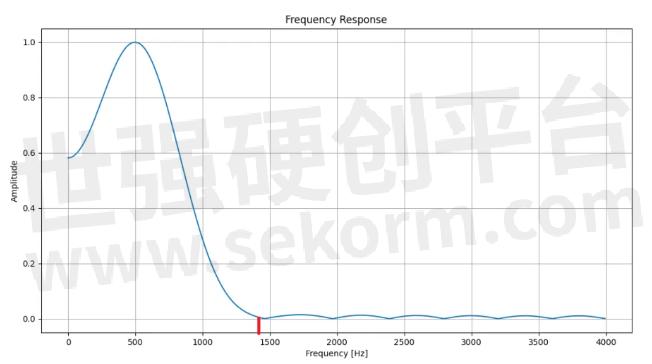
汉明窗滤波器的幅频特性

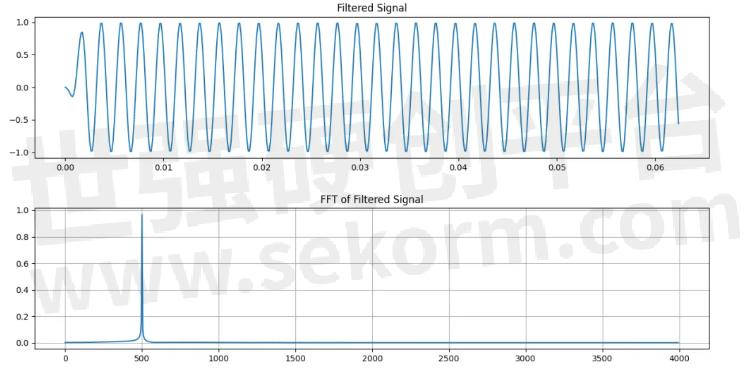
加汉明窗的滤波结果

以上处理为了差异效果，对于滤波器长度、一次处理数据长度，两个信号频率的距离都是作了特别的处理。谁说实际应用中不会碰到呢？

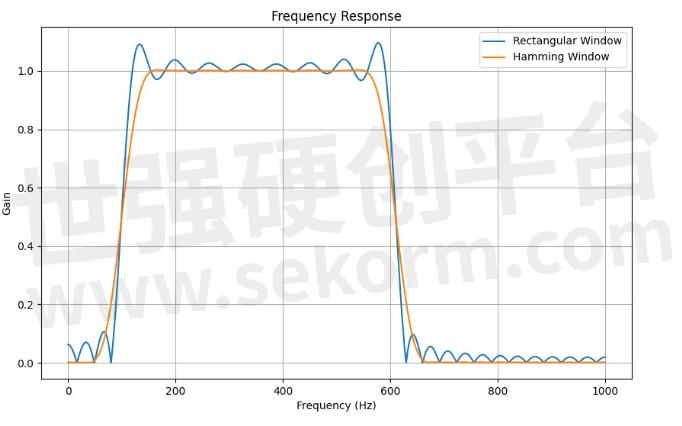
带通滤波器不同的加窗幅频特性

以下内容，都默认已经加窗。

我们再次回到FIR系统使用重叠保留(Overlap-Save)和重叠相加(Overlap-Add)的方式进行分段处理这个话题。

如果FIR系统在频域通过DFT/IDFT并采用重叠保留的方式，那应该是按照下图的方式进行的。

对于FIR滤波器长度为M，数据段长度为L时，流程大致是：在第一个数据段加M-1个0，其余的数据段都是加上前一段的最后M-1个数据；然后进行DFT/IDFT处理得到长度为(L+M-1)的y(n)序列，然后去掉前面M-1个无效值，保留后面的L个[1]。

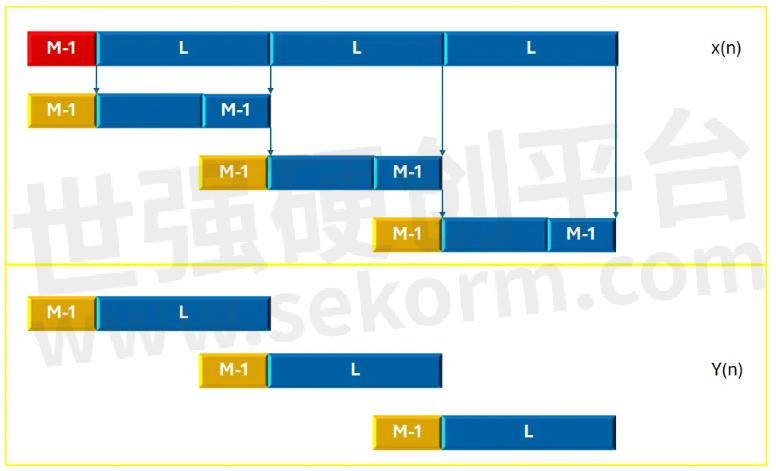
频域中FIR系统的重叠保留法示意图

在时域我们也想照猫画虎的。然而，对于FIR滤波器长度为M和信号的长度L进行卷积，其结果的长度将会是M + L - 1。在实际应用中，我们通常关注的部分是两个序列完全重叠的区域，也就是“有效值”。这意味着如果两个参与卷积的长度不一样（一般L>M)，那最后的“有效值”是需要在卷积的结果序列上两头都要掐掉（M-1）个元素。所以实际卷积结果中的有效序列长度是：

[L+M-1-2（M-1)]=L-M+1

在Python中，卷积函数np.convolve(data_segment, b, mode)对指定长度的数据data_segment（长度L），和FIR滤波器系数序列b（长度M）进行卷积，而输出的结果序列则分为以下三种：

●full：结果长度=M+L-1

●same: 结果长度=max(M,L)

●valid: 结果长度=max(M,L)-min(M,L)+1=L-(M-1)

为了测试时域中的重叠保留处理方式，小编选了上面卷积函数的valid模式。

在重叠保留方式下，每次参与卷积的数据长度不是L，而是每个数据L起始处，都额外添加了（M-1）长的0（第一个）或者前一段数据的最后（M-1）个数据，再与长度为M的滤波器卷积。这种情况下，参与卷积的数据长度和生成的卷积结果长度是有变化的。

1.L和M长序列进行卷积得到的full长度为：M+L-1；

2.那如果将L+(M-1)和M长的序列进行卷积，得到的full长度为：L+(M-1)+M-1=L+2(M-1)；

3.根据步骤2，我们把得到的full长度的结果两边减去(M-1)就可以得到一个长度为L的有效卷积序列值。

所以这个操作和频域中DFT、IDFT之后得到的保留方式有差异，因为时域中卷积之后的分段结果数据的长度会由L+M-1变为L+2(M-1)，最终取卷积有效值段的长度就等于[L+2(M-1)-2(M-1)]=L。

下面提供模拟仿真。输出图和Python模拟代码。（没有画时域卷积中FIR系统的数据长度示意图，无他，偷懒。）

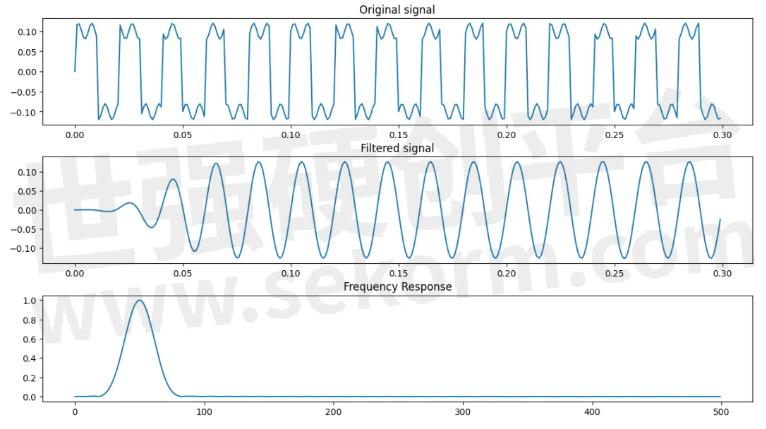
在500Hz信号中混有1400Hz和2400Hz的干扰。采用分段滤波的方式对FIR滤波器进行卷积处理。我们仍然把它命名为“重叠保留法”。

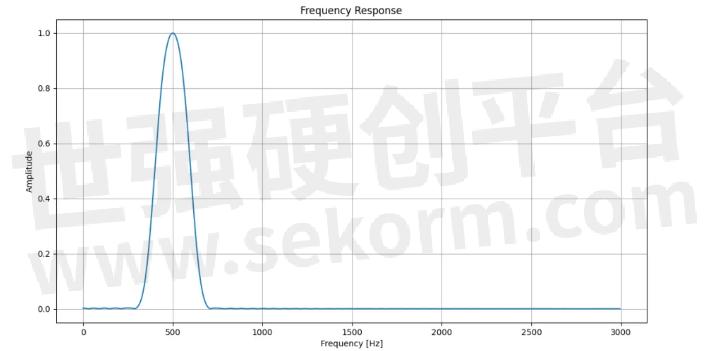
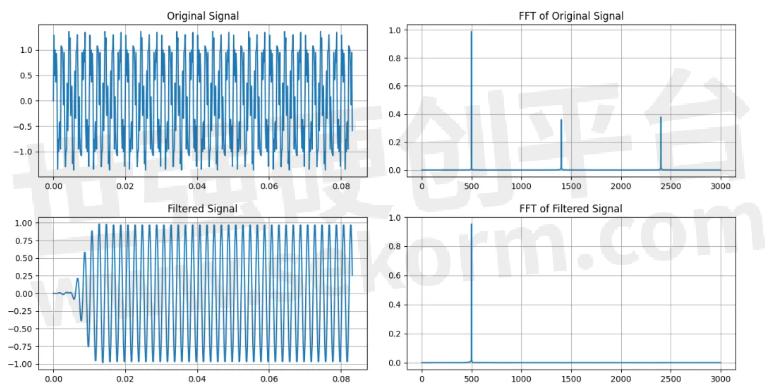
FIR系统时域卷积的重叠保留法

# FIR系统时域卷积：重叠保留法

import numpy as np

import matplotlib.pyplot as plt

from scipy import signal

from scipy.fft import fft,fftfreq

# 设置采样率和数据长度

fs = 6000

# 创建带通滤波器

# Create a bandpass filter

f1 = 400

f2 = 600

filter_len = 100 # FIR滤波器长度

b = signal.firwin(filter_len, [f1, f2], pass_zero=False, fs=fs, window='hamming') #boxcar

# 设置数据长度：模拟每次采集同样长度的数据

# segment_len，是按照np.concatenate函数在Valid模式下卷积后有效长度来计算的

seg_filter_len = 512 # filter output length of each segment data

segment_len = seg_filter_len - filter_len + 1 # 分段数据目标长度 seg_filter_len = segment_len + filter_len - 1

target_length = segment_len * 50 # 总数据长度

# 而新的时间序列的上限

TimeSpace = target_length / fs

# 生成的时间序列为L的整数倍，模拟每次采样的数据的长度

t = np.arange(0, TimeSpace, 1/fs)

# 产生一个含有1.4KHz，2.4KHz和500Hz信号的模拟信号，其中1.4，2.4KHz的信号将被过滤

x = np.sin(2 * np.pi * 500 * t) + 0.5 * np.sin(2 * np.pi * 1400 * t) + 0.5 * np.sin(2 * np.pi * 2400 * t)

# Filter and segment with overlap-save method

# each segment length should be longer than filter's length

y_result = []

segment = None

for i in range(0, target_length, segment_len):

if i==0:

# 第一段数据滤波前，前面填充(M-1)个0，再加开始的L个数据参与滤波卷积

segment = np.concatenate((np.zeros(filter_len-1), x[0:segment_len]))

else:

# 对后续的每个段，包括从上段的末尾取(M-1)个点，再新取L个点，这里M指滤波器长度,L指拟当前新取的数据长度

segment = np.concatenate((x[i-filter_len+1:i], x[i:i+segment_len]))

# 每个段使用“valid”卷积模式，所以每次卷积后的有效数据长度是:L = L + 2(M-1) - 2(M-1) = segment_len

conv = np.convolve(segment, b, mode='valid')

# 与结果进行合并连接

y_result = np.concatenate((y_result, conv))

# Frequency response of filter

w, h = signal.freqz(b, 1, fs=fs)

plt.figure()

plt.plot(w, abs(h))

plt.title('Frequency Response') # 频率响应

plt.xlabel('Frequency [Hz]') # 频率

plt.ylabel('Amplitude') # 幅度

plt.grid()

# Plot the original signal and its FFT

n = len(x)

freq = fftfreq(n, 1/fs)

y = fft(x)

plt.figure(figsize=(9,6))

plt.subplot(221)

plt.plot(t[:500], x[:500])

plt.title('Original Signal') # 原始信号

plt.grid()

plt.subplot(222)

plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 频谱规范化输出

plt.title('FFT of Original Signal') # 原始信号的FFT

plt.grid()

# Plot the filtered signal and its FFT

n = len(y_result)

freq = fftfreq(n, 1/fs)

y = fft(y_result)

plt.subplot(223)

plt.plot(t[:500], y_result[:500])

plt.title('Filtered Signal') # 滤波后的信号

plt.grid()

plt.subplot(224)

plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 频谱规范化输出

plt.title('FFT of Filtered Signal') # 滤波后信号的FFT

plt.grid()

plt.tight_layout()

plt.show()

大胆假设，小心求证。

以上代码并未实证，纯属模拟，各位有兴趣可以试试。

不过安费诺的传感器都是久经沙场，经历过各种工况验证的，感兴趣也可以试试。

FIR时域的“重叠相加”卷积处理，下回分解。

发送到邮箱 |
+1 赞 0
收藏
评论 0
| 转发至：

本文由中国颜值的半壁江山转载自Amphenol Sensors（安费诺传感器学堂公众号），原文标题为:数字滤波器（4）—IIR/FIR系统对连续采集数据的滤波处理和模拟仿真，本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。

全部评论（0）

暂无评论

数字滤波器（5）—FIR连续采样分段卷积时域重叠相加法

我们提到了FIR系统在时域的分段卷积中使用“重叠保留（Overlap-Save）”的处理方式，这里我们说明一下“重叠相加（Overlap-Add）”的处理方式。

技术探讨发布时间 : 2024-08-27

解析数字滤波器（2）——梳状滤波器及相关话题

本文AMPHENOL SENSORS将围绕但不限于梳状滤波器进行展开。其中，梳状滤波器，一方面可以滤除特定的频率（尤其是特定频率的谐波），另一方面也可以在信号中对指定频率及其倍频的信号进行拣选。例如图-1所示的滤除指定谐波成分的梳状滤波器的幅频图。

技术探讨发布时间 : 2024-07-25

解析数字滤波器（1）——陷波滤波器

有鉴于数字信号处理涉及的面太多，我们必须要把话题收缩。数字滤波的种类也是五花八门，因此再选一个小的类型，AMPHENOL SENSORS将围绕离散线性时不变系统来简单讨论一下陷波滤波器（Notch Filter）和梳状滤波器（Comb Filter），通过代码的演示和输出，我们可以比较一下这两类滤波器的特点。在本文中先以陷波滤波器为题来讨论相关的内容。

技术探讨发布时间 : 2024-07-25

Amphenol Sensors(安费诺)/Thermometrics 温度传感器选型指南

目录- 温度传感器产品介绍及应用领域 NTC热敏电阻/PTC热敏电阻探针和组件其他技术和附件

型号- T5D,HM,YA,YB,YC,P60,YD,YF,P65,YG,YH,RL40,YK,YL,YP,YR,EC95,GC32,YS,RL45,GC16,B35,UD20,RL30,3006,AB6,MELF,JA,YS4019,JB,JTC,JC,JD,RL35,JE,JF,MF65,SP85,JS2945,JI,B43,JL,JM,JP,FP10,JR,JTR,CTR100,FP14,P85,JW,M,NDK,T,NDM,CTR65,NDL,ZTP,BB07,PT1000,0706,BB05,NDP,YS4020,NDU,YSM 4021,CL,CTR85,BR16,KU,BR14,KY,BR11,TC,FP07,1403,NHQM,YSM,TH,R100,TM,MA400,PTSM,TP,1803,BB11,EVAP,P100,MA100,DK,SC30,R60,BR23,P20,R65,HVAC,P25,YM120,PT200,EVAPA1450,MS,DKM,MT,CTR60,P30,RL1004,BR32,A1447-A1450,ND,PTA,NK,EVAPA1447,1703,PTE,PTD,SP100,PTF,DC95,PTH,B05,B07,PTO,EVAP A1424,SC50,R85,BR42,C100,2006,JYA,NHQ,NHQMM,GC11,GC14,GE,RL20,M2000,B10,PT100,B14,GT,BR55,MC65,SP60,TK95,SP65,RL14,RL060628,RL10

选型指南 - AMPHENOL SENSORS PDF 中文下载

Amphenol Sensors(安费诺)温度传感器/MEMS压力传感器/C〇2、湿度、灰尘传感器选型指南

目录- Sensors Temperature Sensors Pressure Sensors CO2, Humidity & Dust Sensors

型号- DK SERIES,NDP SERIES,NHQ SERIES,AAS-AQS-UNO-RH-CO2,RL40,T5D SERIES,FMA SERIES,GC32,EC95,AB6 SERIES,RL45,GC16,GT SERIES,DKM SERIES,CTP65,M SERIES,UD20,S SERIES,CTP60,RL30,AIT SERIES,GE-1935,TH SERIES,NDL SERIES,3006,MELF,YS4019,RL35,HM SERIES,GE-2102,GE-2103,JS2945,T6715,T6613-X,AAS-AQS-UNO,TM SERIES,R85 SERIES,SM-UART-04L,YSM SERIES,FP10,NPI-15,T6715-X,FP14,NPC-120,HS12SP,NPI-19,B35 SERIES,T6713,BB07,SUF SERIES,NK SERIES,BB05,YS4020,T6703,YSM 4021,YR SERIES,BR16,A-1737,BR14,T6700,BR11,T SERIES,FP07,1403,NHQM,P85 SERIES,ZTP SERIES,JF SERIES,NDK SERIES,JS8741,NPH SERIES,JS8746,R100,JR SERIES,PTSM,MA400,SM-PWM-01C,JB SERIES,1803,BB11,B05 SERIES,T6616,EVAP,YF SERIES,JA SERIES,P100,YD SERIES,YH SERIES,MF65 SERIES,YG SERIES,MA100,JIC SERIES,YB SERIES,B43 SERIES,T9602,NPC-100,YA SERIES,YC SERIES,SC30,CTP100,BR23,T6613,PTD SERIES,PTE SERIES,YM120,HVAC,JTC SERIES,JTR SERIES,MS SERIES,YK SERIES,WTF083B001,P30 SERIES,YL SERIES,YP SERIES,PTA SERIES,PTH SERIES,ND SERIES,B07 SERIES,PTF SERIES,PTO SERIES,P60 SERIES,JM SERIES,YS SERIES,T6600,RL1004,BR32,JS6780,JI SERIES,HS30P,JW SERIES,A1447-A1450,JS SERIES,TP SERIES,JE SERIES,JC SERIES,GE-1856,1703,B14 SERIES,T6615-X,GE SERIES,R65 SERIES,DC95,JYA SERIES,T3000,EVAP A1424,SC50,BR42,A-1266,C100,GE-1923,NPP-301,706 SERIES,2006,NKA SERIES,AS SERIES,B10 SERIES,P25 SERIES,NHQMM,GC11,RL20,CL SERIES,P20 SERIES,GC14,GE-1920,NPC-1220,JP SERIES,P65 SERIES,ES SERIES,CTP85,T6713-X SERIES,BR55,MC65,KU SERIES,TK95,NDM SERIES,R60 SERIES,NDU SERIES,NPC-1210,TC SERIES,JL SERIES,RL14,JD SERIES,RL060628,RL10

选型指南 - AMPHENOL SENSORS - 05/2019 PDF 英文下载

Amphenol Sensors(安费诺)/All Sensors 压力传感器选型指南（简版）

目录- 传感器解决方案及产品优势介绍传感器技术介绍单芯片压力传感器双芯电路交叉耦合补偿压力传感器双芯电路和气路交叉耦合补偿压力传感器传感器应用领域介绍压力单位换算传感器通用名词解释

型号- DLH,ADCX,ACPC-C,AXCA,ACPC,BLV,DLV,ACPC-H,AXCA-PRIME,AXCA-MIDDLE,MAMP,MLV,SAMP,ACPC-P,BLC,ADUX,BLVR,MAMP-/P,ADCA,DLH,DLVR,DLVR,BLCR,MAMP-P,MDCX,ADO,BLV,AXCX-PRIME-INCH,DLHR,DLHR,AXCX,MLV,AXCA-MIL,BLC,DLC,ADO-MIL

选型指南 - AMPHENOL SENSORS PDF 中文下载

Amphenol Sensors（安费诺）建筑及工业应用传感器选型指南

目录- Chip Cap 2完全校准的温湿度传感器 Telaire Ventostat®T8700壁挂式温湿度变送器 Telaire Ventostat®T8031 CO2小型风管式C02传感器 Telaire®T8041/T8042 分管式C02传感器 Telaire T8100-R系列挂壁式C02和温度变送器（带继电器） Telaire®7000室内空气品质监测器 Telaire VaporstatTM 9002红外露点变送器 Telaire®配件 Telaire HumiTrac™温湿度变送器 T9602湿度与温度传感器 AAS-53系列水管型温度变送器 ADT/AOT/AIT温湿度变送器使用说明书

型号- P40250128,CC2D265,P40250129,P40250126,P40250127,P40250125,P40250122,P40250123,DC95F302W,P40250120,P40250121,T8031,CC2D255,EHR-4,T8100-D-R,P40250139,K53,T8700,CC2A23,PT1000A,AIT,PT1000B,CC2A25,P40250133,P40250131,T2075NG,P40250130,T804K0-10V,T1508,T8200-D-5P,T8042-5VI0-5V,T9602-5-A-1,NI1000,9002,T9602-3-A-1,T5100,P40250149,CC2A35,T8700-E-D,P40250147,0-5000PPM,P40250144,PT100A,T7001I,P40250145,PT100B,P40250142,P40250143,T8100,S4B-EH,CC2A33,P40250141,CC2D235,CC2D355,T7001,PT1000,T2072,T7001D,CC2D25,T9602-3-A,T8042I0-10V,CC2D23,P40250156,T8041,T8100-R,P40250151,T8042,P40250150,T9602-3-D,NTC10K,CC2025,7000,T9602-3-D-1,CC2D35,T9602,CC2D33,ADT,NTC15K,T8200,CC2D335,CHIPCAP 2,NTC10K-II,T2090,T1551,T1552,MPNT3D03750M4,NTC20K,T2007,T8700-D,T8700-E,T8100,T2080,T8100-EC,P40250109,PA0250118,T8100-E-D-GN-5P-R,PA0250115,T1505,P40254275,P40254276,P40254277,P40250189,P40250186,P40250184,P40250185,T8300,P40250182,P40250183,P40250181,AAS-53,8000,PT100,T7001SK,P40250119,NTC10K-A,AOT,P40250117,T9602-5-A,P40250113,P40250114,P40250111,P40250112,DC95F103W,T2076NG,P40250110,P40250193,T9602-5-D,T8001,P40250191,7001D,P40250192,T8002,T9602-5-D-1,MPNV12R30M 16004616,B4B-EH-A,P40250190,T8041-5VI0-5V,RS485,NTC10K-III

选型指南 - AMPHENOL SENSORS PDF 中文下载

OFS-19 Series 介质隔离压力传感器

型号- OFS-19-150A0,OFS-19 SERIES,OFS-19,OFS-19-□□□,OFS-19-102G6

数据手册 - AMPHENOL SENSORS - 2019/12/17 PDF 中文下载

AMPHENOL SENSORS（安费诺）温度传感器选型表

AMPHENOL SENSORS（安费诺）温度传感器选型表。25°C 时阻值：5Ω~1.3MΩ，B25/85：2983K~4793K。

产品型号	品类	安装类型	封装/外壳	25°C 时阻值(Ω)	长度-引线(inch、mm)	工作温度(℃)	电阻容差	B25/85
AL03006-5818-97-G1	温度传感器	通孔	DO-204AH，DO-35，轴向	10k	1.15"（29.20mm）	-50°C ~ 204°C	±10%	3992K

选型表 - AMPHENOL SENSORS 立即选型

【经验】SGX传感器技术电化学气体传感器用电子电路的设计提供指导

本文为Amphenol Sensors旗下SGX传感器技术电化学气体传感器的电子电路设计提供指导。

设计经验发布时间 : 2019-09-21

Amphenol Sensors(安费诺) 汽车传感器选型指南

目录- 汽车传感器解决方案介绍车厢空气质量系列传感器排放处理系列传感器新能源汽车传感器应用测量汽车应用中最为关键的参数

型号- SM-UART-01L,PT200,T6703,TPMS,DPS,G-CAP2,SM-UART-01D,A2103,NPI-19,T6713,A-2102,EGR,A-2103,NPP-301,GE-1935,A-2121,ZTP,DPF,SM-UART-01L+,SM-PWM-01C,NPX1

选型指南 - AMPHENOL SENSORS PDF 中文下载

【经验】一文介绍清楚一次性有创性血压传感器的使用和特点、以及对压力传感的要求

笔者Amphenol Sensors的工程师，本文将对一次性有创性血压传感器的使用及特点，结合国内的医药行业对血压传感器的标准，做一个简单的性能指标上的解说。

设计经验发布时间 : 2020-03-31

Amphenol Sensors(安费诺) 医疗传感器选型指南

目录- NPA贴片式压力传感器系列 NTC AB6 型 "SC/MC"系列专为医疗设汁 MA100系列 ZTP-148SR系列 ZTP-101T系列 NPC-100系列一次性医疗压力传感器 NPC-1210系列 NPG-1220系列中压传感器 NPI-12卫生型压力传感器、不锈钢介质隔离压力传感器 NPI-15系列电流激励高压、介质隔离压力传感器 NPI-15VC系列电压激励、高压、介质隔离压力传感器 NPI-19系列电流激励、中压、介质隔离压力传感器 NPI-19系列电压激励、中压、介质隔离压力传感器 NPP-301系列贴片封装压力传感器

型号- NPP-301B-700AT,NPC-1001000,NPI-12-101G,MC65F103C,NPP-301A-100AT,NPI-19X-YYYZZ,NPI-15X-YYYZZ,NPI-19J-XXX,B35,ZTP-148SR,NPI-19A-XXX,MC65F103A,NPP-301A-200A,MC65F103B,AB6,NPA-300,NPI-19H-XXX,NPA-700,AB6E8,B43,NPP-301B-200A,NPI-12,NPI-19X-XXXXV,NPI-15,SC30F103W,NPP系列,NPP-301B-200AT,SC30F103V,MA100BF103C,NPI-19,SC30F103A,SC,MA100BF103B,MA100BF103A,NPI-15B-XXX,MA100GG232C,NPI-15C-C00903,NNP301B,NNP301A,MA100GG103CN,NPP-301B-700A,BR16,BR14,BR11,NPC-1210XXXX-YZ,ZTP-101T,NPC-100T,MA100GG103BN,MA100,NPP-301A-100A,NPC-100,NPI-19A-C01864,BR23,P20,P25,AB6B4,MC65F232A,MC,AB6B2,MC系列,NPI-19A-002GV,MA100GG103AN,AB6A8-BR16KA103N,NPI-15VC,NPP-301A-200AT,P30,BR32,NPA-100,NPC-1220XXXX-YZ,NPA-500,SC50F103W,NPP-301B-100A,NPA,NPP-301B-100AT,MC65F502B,NPI-15A-XXX,B05,B07,SC30Y103W,NPI-15J-XXX,NPP,NPP-301A-700A,BR42,NPP-301,MA100GG103B,NPI-19B-XXX,NPI-12-101GH,MA100GG103A,MC65G503B,MA100GG103C,NPC-1220,NPP-301A-700AT,B10,NPI-15H-XXX,B14,NPI-15XXXXXX,NTC AB6,BR55,NPC-1210,SC系列

选型指南 - AMPHENOL SENSORS - 2018年7月 PDF 中文下载

数字滤波器(6)—FIR频域连续滤波“重叠相加法”C++源码

传感器和信号处理仅一线之隔，信号的前后端合理搭配，是我们更准确地感知这个世界的一种基本态度和方式。FIR频域重叠相加法还记得我们（此处有重复之嫌）之前的发文《FIR连续采样分段卷积时域重叠相加法》？不过那是在时域处理的模拟和仿真。这次我们的内容是用C++在频域实现的滤波卷积法，仍然是重叠相加法，届时大家可以比较一下两种方式的差异。基本是通过两个处理过程。

设计经验发布时间 : 2024-07-03

有没有氮氧传感器陶瓷芯片？目前本人自研氮氧传感器电控方案已成功，附自研氮氧传感器VS大陆传感器装车测试对比曲线图

世强代理的安费诺旗下SGX品牌的气体传感器，其中MICS-4514可以检测氮氧化合物，请参考：MiCS-4514 a compact MOS sensor Data Sheet【选型】Amphenol Sensors(安费诺)/SGX Sensortech 红外/半导体/电化学/气体传感器传感器选型指南

技术问答发布时间 : 2020-03-30